Graphs of mathematical functions. Functions and graphics. Properties of a power function with exponent a

1. Fractional linear function and its graph

A function of the form y = P(x) / Q(x), where P(x) and Q(x) are polynomials, is called a fractional rational function.

You are probably already familiar with the concept of rational numbers. Likewise rational functions are functions that can be represented as the quotient of two polynomials.

If a fractional rational function is the quotient of two linear functions - polynomials of the first degree, i.e. function of the form

y = (ax + b) / (cx + d), then it is called fractional linear.

Note that in the function y = (ax + b) / (cx + d), c ≠ 0 (otherwise the function becomes linear y = ax/d + b/d) and that a/c ≠ b/d (otherwise the function is constant ). The fractional linear function is defined for all real numbers, except x = -d/c. Graphs of fractional linear functions do not differ in shape from the graph y = 1/x you know. A curve that is a graph of the function y = 1/x is called hyperbole. With an unlimited increase in x absolute value the function y = 1/x decreases indefinitely in absolute value and both branches of the graph approach the x-axis: the right one approaches from above, and the left from below. The lines to which the branches of a hyperbola approach are called its asymptotes.

Example 1.

y = (2x + 1) / (x – 3).

Solution.

Let's select the whole part: (2x + 1) / (x – 3) = 2 + 7/(x – 3).

Now it is easy to see that the graph of this function is obtained from the graph of the function y = 1/x by the following transformations: shift by 3 unit segments to the right, stretching along the Oy axis 7 times and shifting by 2 unit segments upward.

Any fraction y = (ax + b) / (cx + d) can be written in a similar way, highlighting the “integer part”. Consequently, the graphs of all fractional linear functions are hyperbolas, shifted in various ways along the coordinate axes and stretched along the Oy axis.

To construct a graph of any arbitrary fractional linear function It is not at all necessary to transform the fraction defining this function. Since we know that the graph is a hyperbola, it will be enough to find the straight lines to which its branches approach - the asymptotes of the hyperbola x = -d/c and y = a/c.

Example 2.

Find the asymptotes of the graph of the function y = (3x + 5)/(2x + 2).

Solution.

The function is not defined, at x = -1. This means that the straight line x = -1 serves as a vertical asymptote. To find the horizontal asymptote, let’s find out what the values ​​of the function y(x) approach when the argument x increases in absolute value.

To do this, divide the numerator and denominator of the fraction by x:

y = (3 + 5/x) / (2 + 2/x).

As x → ∞ the fraction will tend to 3/2. Means, horizontal asymptote– this is the straight line y = 3/2.

Example 3.

Build graph of a function y = (2x + 1)/(x + 1).

Solution.

Let’s select the “whole part” of the fraction:

(2x + 1) / (x + 1) = (2x + 2 – 1) / (x + 1) = 2(x + 1) / (x + 1) – 1/(x + 1) =

2 – 1/(x + 1).

Now it is easy to see that the graph of this function is obtained from the graph of the function y = 1/x by the following transformations: a shift by 1 unit to the left, a symmetrical display with respect to Ox and a shift by 2 unit segments up along the Oy axis.

Domain D(y) = (-∞; -1)ᴗ(-1; +∞).

Range of values ​​E(y) = (-∞; 2)ᴗ(2; +∞).

Intersection points with axes: c Oy: (0; 1); c Ox: (-1/2; 0). The function increases at each interval of the domain of definition.

Answer: Figure 1.

2. Fractional rational function

Consider a fractional rational function of the form y = P(x) / Q(x), where P(x) and Q(x) are polynomials of degree higher than first.

Examples of such rational functions:

y = (x 3 – 5x + 6) / (x 7 – 6) or y = (x – 2) 2 (x + 1) / (x 2 + 3).

If the function y = P(x) / Q(x) represents the quotient of two polynomials of degree higher than the first, then its graph will, as a rule, be more complex, and it can sometimes be difficult to construct it accurately, with all the details. However, it is often enough to use techniques similar to those we have already introduced above.

Let the fraction be a proper fraction (n< m). Известно, что любую несократимую rational fraction can be represented, and in a unique way, as a sum of a finite number of elementary fractions, the form of which is determined by decomposing the denominator of the fraction Q(x) into the product of real factors:

P(x)/Q(x) = A 1 /(x – K 1) m1 + A 2 /(x – K 1) m1-1 + … + A m1 /(x – K 1) + …+

L 1 /(x – K s) ms + L 2 /(x – K s) ms-1 + … + L ms /(x – K s) + …+

+ (B 1 x + C 1) / (x 2 +p 1 x + q 1) m1 + … + (B m1 x + C m1) / (x 2 +p 1 x + q 1) + …+

+ (M 1 x + N 1) / (x 2 +p t x + q t) m1 + … + (M m1 x + N m1) / (x 2 +p t x + q t).

Obviously, the graph of a fractional rational function can be obtained as the sum of graphs of elementary fractions.

Plotting graphs of fractional rational functions

Let's consider several ways to construct graphs of a fractional rational function.

Example 4.

Draw a graph of the function y = 1/x 2 .

Solution.

We use the graph of the function y = x 2 to construct a graph of y = 1/x 2 and use the technique of “dividing” the graphs.

Domain D(y) = (-∞; 0)ᴗ(0; +∞).

Range of values ​​E(y) = (0; +∞).

There are no points of intersection with the axes. The function is even. Increases for all x from the interval (-∞; 0), decreases for x from 0 to +∞.

Answer: Figure 2.

Example 5.

Graph the function y = (x 2 – 4x + 3) / (9 – 3x).

Solution.

Domain D(y) = (-∞; 3)ᴗ(3; +∞).

y = (x 2 – 4x + 3) / (9 – 3x) = (x – 3)(x – 1) / (-3(x – 3)) = -(x – 1)/3 = -x/ 3 + 1/3.

Here we used the technique of factorization, reduction and reduction to a linear function.

Answer: Figure 3.

Example 6.

Graph the function y = (x 2 – 1)/(x 2 + 1).

Solution.

The domain of definition is D(y) = R. Since the function is even, the graph is symmetrical about the ordinate. Before building a graph, let’s transform the expression again, highlighting the whole part:

y = (x 2 – 1)/(x 2 + 1) = 1 – 2/(x 2 + 1).

Note that isolating the integer part in the formula of a fractional rational function is one of the main ones when constructing graphs.

If x → ±∞, then y → 1, i.e. the straight line y = 1 is a horizontal asymptote.

Answer: Figure 4.

Example 7.

Let's consider the function y = x/(x 2 + 1) and try to accurately find its largest value, i.e. the highest point on the right half of the graph. To accurately construct this graph, today's knowledge is not enough. Obviously, our curve cannot “rise” very high, because the denominator quickly begins to “overtake” the numerator. Let's see if the value of the function can be equal to 1. To do this, we need to solve the equation x 2 + 1 = x, x 2 – x + 1 = 0. This equation has no real roots. This means our assumption is incorrect. To find the most great importance function, you need to find out at what largest A the equation A = x/(x 2 + 1) will have a solution. Let's replace the original equation with a quadratic one: Аx 2 – x + А = 0. This equation has a solution when 1 – 4А 2 ≥ 0. From here we find highest value A = 1/2.

Answer: Figure 5, max y(x) = ½.

Still have questions? Don't know how to graph functions?
To get help from a tutor, register.
The first lesson is free!

website, when copying material in full or in part, a link to the source is required.

1) Function domain and function range.

The domain of a function is the set of all valid valid argument values x(variable x), for which the function y = f(x) determined. The range of a function is the set of all real values y, which the function accepts.

In elementary mathematics, functions are studied only on the set of real numbers.

2) Function zeros.

Function zero is the value of the argument at which the value of the function is equal to zero.

3) Intervals of constant sign of a function.

Intervals of constant sign of a function are sets of argument values ​​on which the function values ​​are only positive or only negative.

4) Monotonicity of the function.

An increasing function (in a certain interval) is a function in which a larger value of the argument from this interval corresponds to a larger value of the function.

A decreasing function (in a certain interval) is a function in which a larger value of the argument from this interval corresponds to a smaller value of the function.

5) Even (odd) function.

An even function is a function whose domain of definition is symmetrical with respect to the origin and for any X from the domain of definition the equality f(-x) = f(x).

The graph of an even function is symmetrical about the ordinate. X An odd function is a function whose domain of definition is symmetrical with respect to the origin and for any from the domain of definition the equality is true f(-x) = - f(x

)..

The graph of an odd function is symmetrical about the origin. 6) Limited and unlimited functions A function is called bounded if there is such a

positive number.

M such that |f(x)| ≤ M for all values ​​of x. If such a number does not exist, then the function is unlimited. 7) Periodicity of the function A function f(x) is periodic if there is a non-zero number T such that for any x from the domain of definition of the function the following holds: f(x+T) = f(x). This smallest number is called the period of the function. All

trigonometric functions are periodic. (Trigonometric formulas). 19. Basic

elementary functions

, their properties and graphs. Application of functions in economics.

Basic elementary functions. Their properties and graphs 1. Linear function.

Linear function is called a function of the form , where x is a variable, a and b are real numbers. Number A is called the slope of the line, it equal to tangent the angle of inclination of this straight line to the positive direction of the x-axis. The graph of a linear function is

straight line

. It is defined by two points.

Properties of a Linear Function

3. The function takes a zero value when or.

4. The function increases (decreases) over the entire domain of definition.

5. A linear function is continuous over the entire domain of definition, differentiable and .

2. Quadratic function.

A function of the form, where x is a variable, coefficients a, b, c are real numbers, is called quadratic

Odds a, b, c determine the location of the graph on the coordinate plane

Coefficient a determines the direction of the branches. The graph of a quadratic function is a parabola. The coordinates of the vertex of the parabola are found using the formulas:

Function properties:

2. A set of values ​​for one of the intervals: or.

3. The function takes zero values ​​when , where the discriminant is calculated by the formula:.

4. The function is continuous over the entire domain of definition and the derivative of the function is equal to .

Build function

We offer to your attention a service for constructing graphs of functions online, all rights to which belong to the company Desmos. Use the left column to enter functions. You can enter manually or using the virtual keyboard at the bottom of the window. To enlarge the window with the graph, you can hide both the left column and the virtual keyboard.

Benefits of online charting

• Visual display of entered functions
• Building very complex graphs
• Construction of graphs specified implicitly (for example, ellipse x^2/9+y^2/16=1)
• The ability to save charts and receive a link to them, which becomes available to everyone on the Internet
• Controlling scale and line color
• Possibility of plotting graphs by points, using constants
• Plotting several function graphs simultaneously
• Plotting in polar coordinates (use r and θ(\theta))

With us it’s easy to build charts of varying complexity online. Construction is done instantly. The service is in demand for finding points of intersection of functions, for depicting graphs for their further movement into Word document as illustrations when solving problems, to analyze the behavioral features of function graphs. The optimal browser for working with charts on this website page is Google Chrome. Correct operation is not guaranteed when using other browsers.

A linear function is a function of the form y=kx+b, where x is the independent variable, k and b are any numbers.
The graph of a linear function is a straight line.

1. To plot a function graph, we need the coordinates of two points belonging to the graph of the function. To find them, you need to take two x values, substitute them into the function equation, and use them to calculate the corresponding y values.

For example, to plot the function y= x+2, it is convenient to take x=0 and x=3, then the ordinates of these points will be equal to y=2 and y=3. We get points A(0;2) and B(3;3). Let's connect them and get a graph of the function y= x+2:

2. In the formula y=kx+b, the number k is called the proportionality coefficient:
if k>0, then the function y=kx+b increases
if k
Coefficient b shows the displacement of the function graph along the OY axis:
if b>0, then the graph of the function y=kx+b is obtained from the graph of the function y=kx by shifting b units upward along the OY axis
if b
The figure below shows graphs of the functions y=2x+3; y= ½ x+3; y=x+3

Note that in all these functions the coefficient k Above zero, and the functions are increasing. Moreover, the greater the value of k, the greater the angle of inclination of the straight line to the positive direction of the OX axis.

In all functions b=3 - and we see that all graphs intersect the OY axis at point (0;3)

Now consider the graphs of the functions y=-2x+3; y=- ½ x+3; y=-x+3

This time in all functions the coefficient k less than zero and functions are decreasing. Coefficient b=3, and the graphs, as in the previous case, intersect the OY axis at point (0;3)

Let's look at the graphs of the functions y=2x+3; y=2x; y=2x-3

Now in all function equations the coefficients k are equal to 2. And we got three parallel lines.

But the coefficients b are different, and these graphs intersect the OY axis at different points:
The graph of the function y=2x+3 (b=3) intersects the OY axis at point (0;3)
The graph of the function y=2x (b=0) intersects the OY axis at the point (0;0) - the origin.
The graph of the function y=2x-3 (b=-3) intersects the OY axis at point (0;-3)

So, if we know the signs of the coefficients k and b, then we can immediately imagine what the graph of the function y=kx+b looks like.
If k 0

If k>0 and b>0, then the graph of the function y=kx+b looks like:

If k>0 and b, then the graph of the function y=kx+b looks like:

If k, then the graph of the function y=kx+b looks like:

If k=0, then the function y=kx+b turns into the function y=b and its graph looks like:

The ordinates of all points on the graph of the function y=b are equal to b If b=0, then the graph of the function y=kx (direct proportionality) passes through the origin:

3. Let us separately note the graph of the equation x=a. The graph of this equation is a straight line parallel to the OY axis, all points of which have an abscissa x=a.

For example, the graph of the equation x=3 looks like this:
Attention! The equation x=a is not a function, so one value of the argument corresponds different meanings functions, which does not correspond to the definition of a function.

4. Condition for parallelism of two lines:

The graph of the function y=k 1 x+b 1 is parallel to the graph of the function y=k 2 x+b 2 if k 1 =k 2

5. The condition for two straight lines to be perpendicular:

The graph of the function y=k 1 x+b 1 is perpendicular to the graph of the function y=k 2 x+b 2 if k 1 *k 2 =-1 or k 1 =-1/k 2

6. Points of intersection of the graph of the function y=kx+b with the coordinate axes.

With OY axis. The abscissa of any point belonging to the OY axis is equal to zero. Therefore, to find the point of intersection with the OY axis, you need to substitute zero in the equation of the function instead of x. We get y=b. That is, the point of intersection with the OY axis has coordinates (0; b).

With OX axis: The ordinate of any point belonging to the OX axis is zero. Therefore, to find the point of intersection with the OX axis, you need to substitute zero in the equation of the function instead of y. We get 0=kx+b. Hence x=-b/k. That is, the point of intersection with the OX axis has coordinates (-b/k;0):

Power function. This is the function: y = axn, Where a, n– permanent. At n= 1 we get direct proportionality: y = ax; n = 2 - at ; n = - 1 - square parabola inverse proportionality or. hyperbole Thus, these functions are special cases of the power function. We know that the zero power of any non-zero number is 1, therefore, at n= 0 the power function turns into a constant value: = y a , i.e. her schedule is straight line, parallel to the axisX, excluding the origin ( clarify please, y= 1 ) Why ? ). All these cases (with (n shown in Fig. 13 0) and Fig. 14 ( < 0). Отрицательные значения nx are not considered here, so

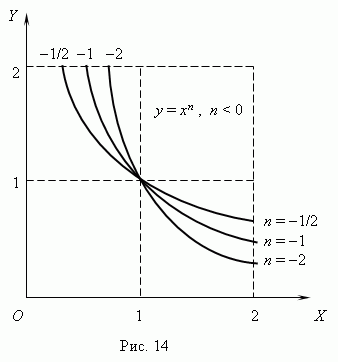
like then some functions: 0) and Fig. 14 (If– integer, power functions make sense even when< 0, но их графики имеют x different kind0) and Fig. 14 (depending on whether even or odd number. n Figure 15 shows two such power functions: n = 3.


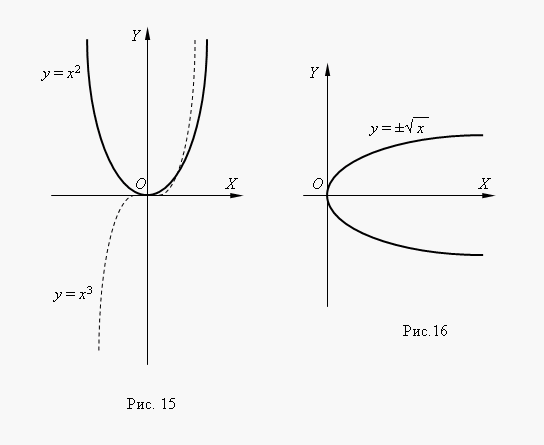
For n= = 2 andAt 2 function is even and its graph is symmetrical. relative to the axis 0) and Fig. 14 (Y Aty = n 3 = 3 the function is odd and its graph is symmetrical relative to the origin coordinates Function.

called cubic parabola Figure 16 shows the function. = 0 the power function turns into a constant value: = n 2 This. function is inverse to a square parabola, its graph is obtained by rotating the graph of a square parabola around the bisector of the 1st coordinate angle This is a way to obtain a graph of any inverse function