How to find vertical horizontal and oblique asymptotes. Asymptotes of the graph of a function. Sloping asymptotes of the graph of a function
The solution can be conveniently divided into two points:
1) First we check whether there are vertical asymptotes. The denominator goes to zero at, and it is immediately clear that at this point the function suffers an infinite discontinuity, and the straight line given by the equation, is the vertical asymptote of the graph of the function. But, before drawing such a conclusion, it is necessary to find one-sided limits:
I remind you of the calculation technique that I similarly focused on in the article Continuity of a function. Breaking points. We substitute “X” in the expression under the limit sign. There is nothing interesting in the numerator:
But the denominator results in an infinitesimal negative number:
It determines the fate of the limit.
The left-hand limit is infinite, and, in principle, it is already possible to make a verdict about the presence of a vertical asymptote. But one-sided limits are needed not only for this - they HELP TO UNDERSTAND HOW the graph of a function is located and to construct it CORRECTLY. Therefore, we must also calculate the right-handed limit:
Conclusion: one-sided limits are infinite, which means that the straight line is the vertical asymptote of the graph of the function at.
The first limit is finite, which means we need to “continue the conversation” and find the second limit:
The second limit is also finite.
Thus, our asymptote is:
Conclusion: the straight line specified by the equation is the horizontal asymptote of the graph of the function at.
To find the horizontal asymptote, you can use a simplified formula:
If there is a finite limit, then the straight line is the horizontal asymptote of the graph of the function at.
It is easy to notice that the numerator and denominator of the function are of the same order of growth, which means that the sought limit will be finite:
According to the condition, there is no need to make a drawing, but if we are in the midst of researching a function, then we immediately make a sketch on the draft:
Based on the three limits found, try to figure out for yourself how the graph of the function might be located. Is it at all difficult? Find 5-6-7-8 points and mark them on the drawing. However, the graph of this function is constructed using graph transformations elementary function, and readers who carefully examined Example 21 of the above article can easily guess what kind of curve this is.
This is an example for independent decision. Let me remind you that the process is conveniently divided into two points - vertical asymptotes and oblique asymptotes. In the sample solution, the horizontal asymptote is found using a simplified scheme.
In practice, fractional-rational functions are most often encountered, and after training on hyperbolas, we will complicate the task:
Find asymptotes of the graph of a function
Solution: One, two and done:
1) Vertical asymptotes are at points of infinite discontinuity, so you need to check whether the denominator goes to zero. Let's decide quadratic equation:
The discriminant is positive, so the equation has two real roots, and the work is added significantly
In order to further find one-sided limits, it is convenient to factorize the square trinomial:
(for compact notation, the “minus” was included in the first bracket). To be on the safe side, let’s check by opening the brackets mentally or on a draft.
Let's rewrite the function in the form
Let's find one-sided limits at the point:
asymptote graph function limit
And at the point:
Thus, the straight lines are vertical asymptotes of the graph of the function in question.
2) If you look at the function, it is quite obvious that the limit will be finite and we have a horizontal asymptote. Let's show its presence in a short way:
Thus, the straight line (abscissa axis) is the horizontal asymptote of the graph of this function.
The found limits and asymptotes provide a lot of information about the graph of the function. Try to mentally imagine the drawing taking into account the following facts:
Sketch your version of the graph on your draft.
Of course, the limits found do not clearly determine the appearance of the graph, and you may make a mistake, but the exercise itself will provide invaluable help during full research functions. The correct picture is at the end of the lesson.
Find asymptotes of the graph of a function
Find asymptotes of the graph of a function
These are tasks for independent solution. Both graphs again have horizontal asymptotes, which are immediately detected by the following features: in Example 4, the order of growth of the denominator is greater than the order of growth of the numerator, and in Example 5, the numerator and denominator are of the same order of growth. In the sample solution, the first function is examined for the presence of oblique asymptotes in full, and the second - through the limit.
Horizontal asymptotes, in my subjective impression, are noticeably more common than those that are “truly tilted.” The long-awaited general case:
Find asymptotes of the graph of a function
Solution: classic of the genre:
- 1) Since the denominator is positive, the function is continuous along the entire number line, and there are no vertical asymptotes. …Is it good? Not the right word - excellent! Point No. 1 is closed.
- 2) Let's check the presence of oblique asymptotes:
The second limit is also finite, therefore, the graph of the function in question has an oblique asymptote:
Thus, when the graph of the function approaches a straight line infinitely close.
Note that it intersects its oblique asymptote at the origin, and such intersection points are quite acceptable - it is important that “everything is normal” at infinity (in fact, this is where we are talking about asymptotes).
Find asymptotes of the graph of a function
Solution: there’s nothing special to comment on, so I’ll draw up an approximate example of a final solution:
1) Vertical asymptotes. Let's explore the point.
The straight line is the vertical asymptote for the graph at.
2) Oblique asymptotes:
The straight line is the slanted asymptote for the graph at.
The found one-sided limits and asymptotes allow us to predict with high confidence what the graph of this function looks like.
Find asymptotes of the graph of a function
This is an example for independent solution; for the convenience of calculating some limits, you can divide the numerator by the denominator term by term. Again, when analyzing your results, try to draw a graph of this function.
Obviously, the owners of “real” oblique asymptotes are the graphs of those fractional rational functions in which the leading degree of the numerator is one greater than the leading degree of the denominator. If it is more, there will no longer be an oblique asymptote (for example).
But other miracles happen in life.
- The concept of asymptotes
One of the important stages of constructing function graphs is the search for asymptotes. We have encountered asymptotes more than once: when constructing graphs of functions, y=tgx, y=сtgx. We defined them as lines that the graph of a function “tends” to, but never crosses. The time has come to give a precise definition of asymptotes.
There are three types of asymptotes: vertical, horizontal and oblique. In the drawing, asymptotes are usually denoted by dotted lines.
Let's consider the following artificially constructed graph of the function (Fig. 16.1), an example of which shows all types of asymptotes:
Let us define each type of asymptote:
1. Direct x=a called vertical asymptote functions if .
2. Direct y=c called horizontal asymptote functions if .
3. Direct y=kx+b called oblique asymptote functions if .
Geometrically, the definition of an oblique asymptote means that at →∞ the graph of the function approaches a straight line as close as desired y=kx+b, i.e. they are almost identical. The difference between practically identical expressions tends to zero.
Note that horizontal and oblique asymptotes are considered only under the condition →∞. Sometimes they are distinguished into horizontal and oblique asymptotes at →+∞ and →-∞.
- Algorithm for searching for asymptotes
To find asymptotes, you can use the following algorithm:
There may be one, several or no vertical asymptotes.
- If c is a number, then y=c– horizontal asymptote;
- If c is infinity, then there are no horizontal asymptotes.
If a function is a ratio of two polynomials, then if the function has horizontal asymptotes, we will not look for oblique asymptotes - they do not exist.
Let's look at examples of finding asymptotes of a function:
Example 16.1. Find the asymptotes of the curve.
Solution X-1≠0; X≠1.
Let's check if the line is straight x= 1 vertical asymptote. To do this, we calculate the limit of the function at the point x= 1: .
x= 1 - vertical asymptote.
With= .
With= = . Because With=2 (number), then y=2– horizontal asymptote.
Since a function is a ratio of polynomials, if there are horizontal asymptotes, we assert that there are no oblique asymptotes.
x= 1 and horizontal asymptote y=2. For clarity, the graph of this function is presented in Fig. 16.2.
Example 16.2. Find the asymptotes of the curve.
Solution. 1. Find the domain of definition of the function: X-2≠0; X≠2.
Let's check if the line is straight x= 2 vertical asymptote. To do this, we calculate the limit of the function at the point x= 2: .
We got that, therefore, x= 2 - vertical asymptote.
2. To search for horizontal asymptotes, we find: With= .
Since uncertainty appears in the limit, we use L'Hopital's rule: With= = . Because With– infinity, then there are no horizontal asymptotes.
3. To search for oblique asymptotes, we find:
We have obtained an uncertainty of the form , let's use L'Hopital's rule: = =1. So, 1. Let's find b according to the formula: .
b= = =
Got that b= 2. Then y=kx+b – oblique asymptote. In our case it looks like: y=x+2.
|
Lecture 17. GENERAL SCHEME FOR STUDYING A FUNCTION AND CONSTRUCTING A GRAPH
In this lecture we will summarize all the previously studied material. The ultimate goal of our long journey is to be able to investigate any analytically. given function and build its schedule. Important parts of our research will be the study of the function for extrema, the determination of intervals of monotonicity, convexity and concavity of the graph, the search for inflection points and asymptotes of the graph of the function.
Taking into account all the above aspects, we present scheme for studying a function and plotting a graph .
1. Find the domain of definition of the function.
2. Examine the function for even-odd parity:
· if , then the function is even (the graph of an even function is symmetrical about the axis OU);
· if , then the function is odd (the graph of an odd function is symmetrical with respect to the origin);
· otherwise the function is neither even nor odd.
3. Investigate the function for periodicity (among the functions we study, only trigonometric functions can be periodic).
4. Find the intersection points of the function graph with the coordinate axes:
· Oh: at=0 (we solve the equation only if we can use methods known to us);
· OU: X=0.
5. Find the first derivative of the function and critical points of the first kind.
6. Find monotonicity intervals and extrema of the function.
7. Find the second derivative of the function and critical points of the second kind.
8. Find the convexity-concavity intervals of the function graph and inflection points.
9. Find the asymptotes of the graph of the function.
10. Construct a graph of the function. When constructing, you should take into account cases of possible location of the graph near asymptotes :
11. If necessary, select control points for more accurate construction.
Let's consider a scheme for studying a function and constructing its graph using specific examples:
Example 17.1. Graph the function.
Solution. 1. This function is defined on the entire number line except X=3, because at this point the denominator goes to zero.
2. To determine whether a function is even or odd, we find:
We see that and , therefore, is neither an even nor an odd function.
3. The function is non-periodic.
4. Find the points of intersection with the coordinate axes. To find the point of intersection with the axis Oh let's accept at=0. We get the equation: . So, point (0; 0) is the point of intersection with the coordinate axes.
5. Let's find the derivative of the function using the rule of differentiation of fractions: = = = = .
To find critical points, we find the points at which the derivative of the function is equal to 0 or does not exist.
If =0, therefore . The product is then equal to 0 when at least one of the factors is equal to 0: or .
X-3) 2 is equal to 0, i.e. does not exist when X=3.
So, the function has three critical points of the first kind: ; ; .
6. On the numerical axis we mark critical points of the first kind, and we mark the point with a punctured dot, because the function is not defined in it.
We place the derivative = signs on each interval:
|
|
On intervals where , the original function increases (at (-∞;0]), where - decreases (at ).
Dot X=0 is the maximum point of the function. To find the maximum of the function, we find the value of the function at point 0: .
Dot X=6 is the minimum point of the function. To find the minimum of the function, we find the value of the function at point 6: .
The research results can be entered into a table. The number of rows in the table is fixed and equal to four, and the number of columns depends on the function being studied. In the cells of the first line, intervals are sequentially entered into which the critical points divide the domain of definition of the function, including the critical points themselves. To avoid errors when constructing points that do not belong to the definition domain, you can not include them in the table.
The second line of the table contains the signs of the derivative on each of the intervals under consideration and the value of the derivative at critical points. In accordance with the signs of the derivative of the function, the intervals of increase, decrease, and extrema of the function are marked in the third line.
The last line serves to indicate the maximum and minimum of the function.
| X | (-∞;0) | (0;3) | (3;6) | (6;+ ∞) | |||
| + | - | - | + | ||||
| f(x) | |||||||
| conclusions | max | min |
7. Let’s find the second derivative of the function as the derivative of the first derivative: = =
Let's put it in the numerator X-3 for brackets and perform the reduction:
Let us present similar terms in the numerator: .
Let's find critical points of the second kind: points at which the second derivative of the function is equal to zero or does not exist.
0 if =0. This fraction cannot equal zero, therefore, there are no points at which the second derivative of the function equals zero.
Does not exist if denominator ( X-3) 3 is equal to 0, i.e. does not exist when X=3. OU:Oh ,
, origin, units of measurement for each axis.
Before plotting a function, you need to:
Draw the asymptotes with dotted lines;
|
mark the maximum and minimum of the function, and it is recommended to indicate the maximum and minimum of the function directly on the drawing with arcs: k or ;
· using the obtained data on the intervals of increase, decrease, convexity and concavity, construct a graph of the function. The branches of the graph should “tend” to asymptotes, but not intersect them.
· check whether the graph of the function corresponds to the research conducted: if the function is even or odd, then whether the symmetry is observed; Do the intervals of increase and decrease, convexity and concavity, and inflection points correspond to the theoretically found ones?
11. For more accurate construction, you can select several control points. For example, let's find the function values at points -2 and 7:
We adjust the schedule taking into account control points.
- Control questions:
- What is the algorithm for graphing a function?
CHAPTER 3. 3. INTEGRAL CALCULUS OF A FUNCTION
How many asymptotes can the graph of a function have?
Not one, one, two, three,... or infinitely many. We won’t go far for examples; let’s remember the elementary functions. A parabola, a cubic parabola, and a sine wave do not have asymptotes at all. exponential graph, logarithmic function has a unique asymptote. The arctangent and arccotangent have two of them, and the tangent and cotangent have infinitely many. It is not uncommon for a graph to have both horizontal and vertical asymptotes. Hyperbole, will always love you.
What does it mean to find the asymptotes of the graph of a function?
This means figuring out their equations, and drawing straight lines if the problem requires it. The process involves finding the limits of a function.
Vertical asymptotes of the graph of a function
The vertical asymptote of the graph, as a rule, is located at the point of infinite discontinuity of the function. It's simple: if at a point the function suffers an infinite discontinuity, then the straight line specified by the equation is the vertical asymptote of the graph.
Note: Please note that the entry is used to refer to two completely different concepts. Whether a point is implied or an equation of a line depends on the context.
Thus, to establish the presence of a vertical asymptote at a point, it is enough to show that at least one of the one-sided limits is infinite. Most often this is the point where the denominator of the function is zero. Essentially, we have already found vertical asymptotes in the last examples of the lesson on continuity of a function. But in some cases there is only one one-sided limit, and if it is infinite, then again - love and favor the vertical asymptote. The simplest illustration: and the ordinate axis.
From the above, an obvious fact also follows: if the function is continuous on, then there are no vertical asymptotes. For some reason a parabola came to mind. Really, where can you “stick” a straight line here? ...yes... I understand... Uncle Freud's followers became hysterical =)
The converse statement is generally false: for example, the function is not defined on the entire number line, but is completely deprived of asymptotes.
Sloping asymptotes of the graph of a function
Oblique (as special case- horizontal) asymptotes can be drawn if the argument of the function tends to “plus infinity” or to “minus infinity”. Therefore, the graph of a function cannot have more than 2 inclined asymptotes. For example, the graph of an exponential function has a single horizontal asymptote at, and the graph of the arctangent at has two such asymptotes, and different ones at that.
When the graph in both places approaches a single oblique asymptote, it is customary to combine the “infinities” under a single entry. For example, ...you guessed correctly: .
This is exactly how the typical task is formulated, and it involves finding ALL asymptotes of the graph (vertical, inclined/horizontal). Although, to be more precise in posing the question, we are talking about research for the presence of asymptotes (after all, there may not be any at all).
Let's start with something simple:
Example 1
Solution It’s convenient to break it down into two points:
1) First we check whether there are vertical asymptotes. The denominator goes to zero at , and it is immediately clear that at this point the function suffers endless gap, and the straight line given by the equation is the vertical asymptote of the graph of the function. But, before drawing such a conclusion, it is necessary to find one-sided limits: 
I remind you of the calculation technique that I similarly focused on in the article continuity of function. Break points. In the expression under the limit sign we substitute . There is nothing interesting in the numerator:
.
But in the denominator it turns out infinitesimal negative number:
, it determines the fate of the limit.
The left-hand limit is infinite, and, in principle, it is already possible to make a verdict about the presence of a vertical asymptote. But one-sided limits are needed not only for this - they HELP TO UNDERSTAND HOW locate the graph of the function and build it CORRECTLY. Therefore, we must also calculate the right-handed limit: 
Conclusion: one-sided limits are infinite, which means that the straight line is the vertical asymptote of the graph of the function at .
First limit finite, which means it is necessary to “continue the conversation” and find the second limit:
The second limit too finite.
Thus, our asymptote is:
Conclusion: the straight line given by the equation is the horizontal asymptote of the graph of the function at .
To find the horizontal asymptote you can use a simplified formula:
If there is a finite limit, then the straight line is the horizontal asymptote of the graph of the function at .
It is easy to see that the numerator and denominator of the function same order of growth, which means the sought limit will be finite: 
Answer:
According to the condition, you do not need to complete the drawing, but if in full swing function study, then on the draft we immediately make a sketch: 
Based on the three found limits, try to figure out for yourself how the graph of the function might be located. Is it at all difficult? Find 5-6-7-8 points and mark them on the drawing. However, the graph of this function is constructed using transformations of the graph of an elementary function, and readers who carefully examined Example 21 of the above article can easily guess what kind of curve this is.
Example 2
Find asymptotes of the graph of a function
This is an example for you to solve on your own. Let me remind you that the process is conveniently divided into two points - vertical asymptotes and oblique asymptotes. In the sample solution, the horizontal asymptote is found using a simplified scheme.
In practice, fractional-rational functions are most often encountered, and after training on hyperbolas, we will complicate the task:
Example 3
Find asymptotes of the graph of a function 
Solution: One, two and done:
1) Vertical asymptotes are located at points of infinite discontinuity, so you need to check whether the denominator goes to zero. Let's decide quadratic equation :
The discriminant is positive, so the equation has two real roots, and the work is significantly increased =) 
In order to further find one-sided limits, it is convenient to factorize the square trinomial:
(for compact notation, the “minus” was included in the first bracket). To be on the safe side, let’s check by opening the brackets mentally or on a draft.
Let's rewrite the function in the form 
Let's find one-sided limits at the point: 
And at the point: 
Thus, the straight lines are vertical asymptotes of the graph of the function in question.
2) If you look at the function 
, then it is quite obvious that the limit will be finite and we have a horizontal asymptote. Let's show its presence in a short way: 
Thus, the straight line (abscissa axis) is the horizontal asymptote of the graph of this function.
Answer:
The found limits and asymptotes provide a lot of information about the graph of the function. Try to mentally imagine the drawing taking into account the following facts: 
Sketch your version of the graph on your draft.
Of course, the limits found do not clearly determine the appearance of the graph, and you may make a mistake, but the exercise itself will provide invaluable help during full function study. The correct picture is at the end of the lesson.
Example 4
Find asymptotes of the graph of a function
Example 5
Find asymptotes of the graph of a function 
These are tasks for independent solution. Both graphs again have horizontal asymptotes, which are immediately detected by the following features: in Example 4 growth order denominator is greater than the order of growth of the numerator, and in Example 5 the numerator and denominator same order of growth. In the sample solution, the first function is examined for the presence of oblique asymptotes in full, and the second - through the limit.
Horizontal asymptotes, in my subjective impression, are noticeably more common than those that are “truly tilted.” The long-awaited general case:
Example 6
Find asymptotes of the graph of a function 
Solution: classics of the genre:
1) Since the denominator is positive, then the function continuous along the entire number line, and there are no vertical asymptotes. …Is it good? Not the right word - excellent! Point No. 1 is closed.
2) Let's check the presence of oblique asymptotes:
First limit finite, so let's move on. During the calculation of the second limit to eliminate uncertainty "infinity minus infinity" We bring the expression to a common denominator: 
The second limit too finite Therefore, the graph of the function in question has an oblique asymptote:
Conclusion:
Thus, when the graph of the function infinitely close approaches a straight line: 
Note that it intersects its oblique asymptote at the origin, and such intersection points are quite acceptable - it is important that “everything is normal” at infinity (in fact, this is where we are talking about asymptotes).
Example 7
Find asymptotes of the graph of a function
Solution: There’s nothing special to comment on, so I’ll draw up an approximate example of a clean solution:
1) Vertical asymptotes. Let's explore the point. 
The straight line is the vertical asymptote for the graph at .
2) Oblique asymptotes: 
The straight line is the slanted asymptote for the graph at .
Answer: 
The found one-sided limits and asymptotes allow us to predict with high confidence what the graph of this function looks like. Correct drawing at the end of the lesson.
Example 8
Find asymptotes of the graph of a function
This is an example for independent solution; for the convenience of calculating some limits, you can divide the numerator by the denominator term by term. Again, when analyzing your results, try to draw a graph of this function.
Obviously, the owners of “real” oblique asymptotes are the graphs of those fractional rational functions whose highest degree of numerator one more the highest degree of the denominator. If it is more, there will no longer be an oblique asymptote (for example, ).
But other miracles happen in life:
Example 9
Solution: function continuous on the entire number line, which means there are no vertical asymptotes. But there may well be inclined ones. We check:
I remember how I encountered a similar function back in university and simply could not believe that it had an oblique asymptote. Until I calculated the second limit:
Strictly speaking, there are two uncertainties here: and , but one way or another, you need to use the solution method, which is discussed in Examples 5-6 of the article about the limits increased complexity . We multiply and divide by the conjugate expression to use the formula:
Answer:
Perhaps the most popular oblique asymptote.
Until now, infinity has been “cut with the same brush,” but it happens that the graph of the function two different oblique asymptotes at and at:
Example 10
Examine the graph of a function for the presence of asymptotes 
Solution: the radical expression is positive, which means domain- any number is valid, and there cannot be vertical sticks.
Let's check whether oblique asymptotes exist.
If “x” tends to “minus infinity”, then:
(when entering an “X” under Square root it is necessary to add a minus sign so as not to lose the negativity of the denominator)
It looks unusual, but here the uncertainty is “infinity minus infinity.” Multiply the numerator and denominator by the conjugate expression:
Thus, the straight line is the slanted asymptote of the graph at .
With “plus infinity” everything is more trivial: 
And the straight line is at .
Answer:
If ;
, If .
I can't resist graphic image:
This is one of the branches hyperboles .
It is not uncommon for the potential availability of asymptotes to be initially limited domain of the function:
Example 11
Examine the graph of a function for the presence of asymptotes
Solution: it's obvious that 
, therefore we consider only the right half-plane, where there is a graph of the function.
1) Function continuous on the interval , which means that if a vertical asymptote exists, then it can only be the ordinate axis. Let's study the behavior of the function near the point on right:
Note, there is NO uncertainty here(such cases were emphasized at the beginning of the article Methods for solving limits).
Thus, the straight line (ordinate axis) is the vertical asymptote for the graph of the function at .
2) The study on oblique asymptote can be carried out according to the full scheme, but in the article L'Hopital Rules we found out that linear function more high order growth than logarithmic, therefore: 
(See Example 1 of the same lesson).
Conclusion: the x-axis is the horizontal asymptote of the graph of the function at .
Answer:
If ;
, If .
Drawing for clarity: 
It is interesting that a seemingly similar function has no asymptotes at all (those who wish can check this).
Two final examples for self-study:
Example 12
Examine the graph of a function for the presence of asymptotes 
To check for vertical asymptotes, you first need to find domain of a function, and then calculate a couple of one-sided limits at the “suspicious” points. Oblique asymptotes are also not excluded, since the function is defined at “plus” and “minus” infinity.
Example 13
Examine the graph of a function for the presence of asymptotes
But here there can only be oblique asymptotes, and the directions should be considered separately.
I hope you found the right asymptote =)
I wish you success!
Solutions and answers:
Example 2:Solution
:
. Let's find one-sided limits:
Straight is the vertical asymptote of the graph of the function at .
2) Oblique asymptotes.
Straight .
Answer:
Drawing
to Example 3:
Example 4:Solution
:
1) Vertical asymptotes. The function suffers an infinite break at a point . Let's calculate one-sided limits:
Note: an infinitesimal negative number to an even power is equal to an infinitesimal positive number:
.
Straight is the vertical asymptote of the graph of the function.
2) Oblique asymptotes.
Straight (abscissa axis) is the horizontal asymptote of the graph of the function at .
Answer:
Asymptotes of the graph of a function
The ghost of the asymptote has been wandering around the site for a long time to finally materialize in a separate article and bring particular delight to readers who are puzzled full study of the function. Finding the asymptotes of a graph is one of the few parts of this task that is covered in school course only in overview, since events revolve around calculation function limits, but they still relate to higher mathematics. For visitors who have little understanding of mathematical analysis, I think the hint is clear ;-) ...stop, stop, where are you going? Limits- it's easy!
Examples of asymptotes were encountered immediately in the first lesson about graphs of elementary functions, and the topic is now receiving detailed consideration.
So what is an asymptote?
Imagine variable point, which “travels” along the graph of the function. Asymptote is straight, to whcih indefinitely close the graph of a function approaches as its variable point moves to infinity.
Note : definition is meaningful if you need formulation in notation mathematical analysis, please refer to the tutorial.
On the plane, asymptotes are classified according to their natural location:
1) Vertical asymptotes, which are given by an equation of the form , where “alpha” is real number. A popular representative defines the ordinate axis itself,
with a slight feeling of nausea we remember the hyperbole.
2) Oblique asymptotes traditionally written equation of a straight line with an angle coefficient. Sometimes a special case is identified as a separate group - horizontal asymptotes. For example, the same hyperbola with asymptote.
Let's go quickly, let's hit the topic with a short burst of machine gun fire:
How many asymptotes can the graph of a function have?
Not one, one, two, three,... or infinitely many. We won’t go far for examples, let’s remember elementary functions. A parabola, a cubic parabola, and a sine wave do not have asymptotes at all. The graph of an exponential, logarithmic function has a single asymptote. The arctangent and arccotangent have two of them, and the tangent and cotangent have infinitely many. It is not uncommon for a graph to have both horizontal and vertical asymptotes. Hyperbole, will always love you.
What means ?
Vertical asymptotes of the graph of a function
The vertical asymptote of the graph is usually located at the point of infinite discontinuity functions. It's simple: if at a point the function suffers an infinite discontinuity, then the straight line specified by the equation is the vertical asymptote of the graph.
Note : Note that the entry is used to refer to two completely different concepts. Whether a point is implied or an equation of a line depends on the context.
Thus, to establish the presence of a vertical asymptote at a point, it is enough to show that at least one from one-sided limits 
infinite. Most often this is the point where the denominator of the function is zero. Essentially, we have already found vertical asymptotes in the last examples of the lesson on the continuity of a function. But in some cases there is only one one-sided limit, and if it is infinite, then again - love and favor the vertical asymptote. The simplest illustration: and the ordinate axis (see. Graphs and properties of elementary functions).
From the above, an obvious fact also follows: if the function is continuous on, then there are no vertical asymptotes. For some reason a parabola came to mind. Really, where can you “stick” a straight line here? ...yes... I understand... Uncle Freud's followers became hysterical =)
The converse statement is generally false: for example, the function is not defined on the entire number line, but is completely deprived of asymptotes.
Sloping asymptotes of the graph of a function
Oblique (as a special case - horizontal) asymptotes can be drawn if the argument of the function tends to “plus infinity” or to “minus infinity”. That's why the graph of a function cannot have more than two slanting asymptotes. For example, the graph of an exponential function has a single horizontal asymptote at , and the graph of the arctangent at has two such asymptotes, and different ones at that.
When the graph in both places approaches a single oblique asymptote, then the “infinities” are usually combined under a single entry. For example, ...you guessed correctly: .
General rule of thumb :
If there are two final limit 
, then the straight line is the oblique asymptote of the graph of the function at . If at least one of the listed limits is infinite, then there is no oblique asymptote.
Note : the formulas remain valid if “x” tends only to “plus infinity” or only to “minus infinity”.
Let us show that the parabola has no oblique asymptotes: 
The limit is infinite, which means there is no oblique asymptote. Note that in finding the limit 
the need has disappeared since the answer has already been received.
Note
: If you have (or will have) difficulties understanding the plus-minus, minus-plus signs, please see the help at the beginning of the lesson
on infinitesimal functions, where I told you how to correctly interpret these signs.
It is obvious that for any quadratic, cubic function, polynomial of the 4th and higher degrees there are also no oblique asymptotes.
Now let’s make sure that the graph also does not have an oblique asymptote. To reveal uncertainty we use L'Hopital's rule:
, which was what needed to be checked.
When the function grows indefinitely, but there is no straight line to which its graph would approach infinitely close.
Let's move on to the practical part of the lesson:
How to find the asymptotes of the graph of a function?
This is exactly how the typical task is formulated, and it involves finding ALL asymptotes of the graph (vertical, inclined/horizontal). Although, to be more precise in posing the question, we are talking about research for the presence of asymptotes (after all, there may not be any at all). Let's start with something simple:
Example 1
Find asymptotes of the graph of a function
Solution It’s convenient to break it down into two points:
1) First we check whether there are vertical asymptotes. The denominator goes to zero at , and it is immediately clear that at this point the function suffers endless gap, and the straight line given by the equation is the vertical asymptote of the graph of the function. But, before drawing such a conclusion, it is necessary to find one-sided limits: 
I remind you of the calculation technique that I similarly focused on in the article Continuity of function. Break points. In the expression under the limit sign we substitute . There is nothing interesting in the numerator:
.
But in the denominator it turns out infinitesimal negative number:
, it determines the fate of the limit.
The left-hand limit is infinite, and, in principle, it is already possible to make a verdict about the presence of a vertical asymptote. But one-sided limits are needed not only for this - they HELP TO UNDERSTAND HOW locate the graph of the function and build it CORRECTLY. Therefore, we must also calculate the right-handed limit: 
Conclusion: one-sided limits are infinite, which means that the straight line is the vertical asymptote of the graph of the function at .
First limit finite, which means it is necessary to “continue the conversation” and find the second limit:
The second limit too finite.
Thus, our asymptote is:
Conclusion: the straight line given by the equation is the horizontal asymptote of the graph of the function at .
To find the horizontal asymptote
you can use a simplified formula:
If exists finite limit, then the straight line is the horizontal asymptote of the graph of the function at .
It is easy to see that the numerator and denominator of the function same order of growth, which means the sought limit will be finite: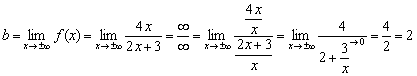 
Answer:
According to the condition, you do not need to complete the drawing, but if in full swing function study, then on the draft we immediately make a sketch: 
Based on the three found limits, try to figure out for yourself how the graph of the function might be located. Is it at all difficult? Find 5-6-7-8 points and mark them on the drawing. However, the graph of this function is constructed using transformations of the graph of an elementary function, and readers who carefully examined Example 21 of the above article can easily guess what kind of curve this is.
Example 2
Find asymptotes of the graph of a function
This is an example for you to solve on your own. Let me remind you that it is convenient to divide the process into two points – vertical asymptotes and oblique asymptotes. In the sample solution, the horizontal asymptote is found using a simplified scheme.
In practice, fractional-rational functions are most often encountered, and after training on hyperbolas, we will complicate the task:
Example 3
Find asymptotes of the graph of a function 
Solution: One, two and done:
1) Vertical asymptotes are located at points of infinite discontinuity, so you need to check whether the denominator goes to zero. Let's decide quadratic equation:
The discriminant is positive, so the equation has two real roots, and the work is significantly increased =) 
In order to further find one-sided limits, it is convenient to factorize the square trinomial:
(for compact notation, the “minus” was included in the first bracket). To be on the safe side, let’s check by opening the brackets mentally or on a draft.
Let's rewrite the function in the form 
Let's find one-sided limits at the point: 
And at the point: 
Thus, the straight lines are vertical asymptotes of the graph of the function in question.
2) If you look at the function 
, then it is quite obvious that the limit will be finite and we have a horizontal asymptote. Let's show its presence in a short way: 
Thus, the straight line (abscissa axis) is the horizontal asymptote of the graph of this function.
Answer:
The found limits and asymptotes provide a lot of information about the graph of the function. Try to mentally imagine the drawing taking into account the following facts: 
Sketch your version of the graph on your draft.
Of course, the limits found do not clearly determine the appearance of the graph, and you may make a mistake, but the exercise itself will provide invaluable help during full function study. The correct picture is at the end of the lesson.
Example 4
Find asymptotes of the graph of a function
Example 5
Find asymptotes of the graph of a function 
These are tasks for independent solution. Both graphs again have horizontal asymptotes, which are immediately detected by the following features: in Example 4 growth order denominator more, than the order of growth of the numerator, and in Example 5 the numerator and denominator same order of growth. In the sample solution, the first function is examined for the presence of oblique asymptotes in full, and the second – through the limit.
Horizontal asymptotes, in my subjective impression, are noticeably more common than those that are “truly tilted.” The long-awaited general case:
Example 6
Find asymptotes of the graph of a function 
Solution: classics of the genre:
1) Since the denominator is positive, then the function continuous along the entire number line, and there are no vertical asymptotes. …Is it good? Not the right word - excellent! Point No. 1 is closed.
2) Let's check the presence of oblique asymptotes:
First limit finite, so let's move on. During the calculation of the second limit to eliminate uncertainty "infinity minus infinity" We bring the expression to a common denominator: 
The second limit too finite Therefore, the graph of the function in question has an oblique asymptote:
Conclusion:
Thus, when the graph of the function 
infinitely close approaches a straight line: 
Note that it intersects its oblique asymptote at the origin, and such intersection points are quite acceptable - it is important that “everything is normal” at infinity (in fact, this is where we are talking about asymptotes).
Example 7
Find asymptotes of the graph of a function
Solution: There’s nothing special to comment on, so I’ll draw up an approximate example of a clean solution:
1) Vertical asymptotes. Let's explore the point. 
The straight line is the vertical asymptote for the graph at .
2) Oblique asymptotes: 
The straight line is the slanted asymptote for the graph at .
Answer: 
The found one-sided limits and asymptotes allow us to predict with high confidence what the graph of this function looks like. Correct drawing at the end of the lesson.
Example 8
Find asymptotes of the graph of a function
This is an example for independent solution; for the convenience of calculating some limits, you can divide the numerator by the denominator term by term. Again, when analyzing your results, try to draw a graph of this function.
Obviously, the owners of “real” oblique asymptotes are the graphs of those fractional rational functions whose highest degree of numerator one more the highest degree of the denominator. If it is more, there will be no oblique asymptote (for example, ).
But other miracles happen in life:
Example 9
Example 11
Examine the graph of a function for the presence of asymptotes
Solution: it's obvious that 
, therefore we consider only the right half-plane, where there is a graph of the function.
Thus, the straight line (ordinate axis) is the vertical asymptote for the graph of the function at .
2) The study on oblique asymptote can be carried out according to the full scheme, but in the article L'Hopital's rules we found out that a linear function has a higher order of growth than a logarithmic one, therefore: 
(See Example 1 of the same lesson).
Conclusion: the x-axis is the horizontal asymptote of the graph of the function at .
Answer:
, If ;
, If .
Drawing for clarity: 
It is interesting that a seemingly similar function has no asymptotes at all (those who wish can check this).
Two final examples for self-study:
Example 12
Examine the graph of a function for the presence of asymptotes 