Как найти вертикальные горизонтальные и наклонные асимптоты. Асимптоты графика функции. Наклонные асимптоты графика функции
Решение удобно разбить на два пункта:
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при, и сразу понятно, что в данной точке функция терпит бесконечный разрыв, а прямая, заданная уравнением, является вертикальной асимптотой графика функции. Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Напоминаю технику вычислений, на которой я подобно останавливался в статье Непрерывность функции. Точки разрыва. В выражение под знаком предела вместо «икса» подставляем. В числителе ничего интересного:
А вот в знаменателе получается бесконечно малое отрицательное число:
Оно и определяет судьбу предела.
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого - они ПОМОГАЮТ ПОНЯТЬ, КАК расположен график функции и построить его КОРРЕКТНО. Поэтому обязательно вычислим и правосторонний предел:
Вывод: односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при.
Первый предел конечен, значит, необходимо «продолжить разговор» и найти второй предел:
Второй предел тоже конечен.
Таким образом, наша асимптота:
Вывод: прямая, заданная уравнением является горизонтальной асимптотой графика функции при.
Для нахождения горизонтальной асимптоты можно пользоваться упрощенной формулой:
Если существует конечный предел, то прямая является горизонтальной асимптотой графика функции при.
Нетрудно заметить, что числитель и знаменатель функции одного порядка роста, а значит, искомый предел будет конечным:
По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции, то на черновике сразу же делаем набросок:
Исходя из трёх найденных пределов, попытайтесь самостоятельно прикинуть, как может располагаться график функции. Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции, и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта - вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдёна по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Найти асимптоты графика функции
Решение: Раз, два и готово:
1) Вертикальные асимптоты находятся в точках бесконечного разрыва, поэтому нужно проверить, обращается ли знаменатель в ноль. Решим квадратное уравнение:
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется
В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители:
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
Перепишем функцию в виде
Найдём односторонние пределы в точке:
асимптота график функция предел
И в точке:
Таким образом, прямые являются вертикальными асимптотами графика рассматриваемой функции.
2) Если посмотреть на функцию, то совершенно очевидно, что предел будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
Таким образом, прямая (ось абсцисс) является горизонтальной асимптотой графика данной функции.
Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:
Схематично изобразите вашу версию графика на черновике.
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции. Правильная картинка - в конце урока.
Найти асимптоты графика функции
Найти асимптоты графика функции
Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4порядок роста знаменателя больше, чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста. В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая - через предел.
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Найти асимптоты графика функции
Решение: классика жанра:
- 1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово - отлично! Пункт №1 закрыт.
- 2) Проверим наличие наклонных асимптот:
Второй предел тоже конечен, следовательно, у графика рассматриваемой функции существует наклонная асимптота:
Таким образом, при график функции бесконечно близко приближается к прямой.
Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы - важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
Найти асимптоты графика функции
Решение: комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные асимптоты. Исследуем точку.
Прямая является вертикальной асимптотой для графика при.
2) Наклонные асимптоты:
Прямая является наклонной асимптотой для графика при.
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции.
Найти асимптоты графика функции
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше - наклонной асимптоты уже не будет (например,).
Но в жизни происходят и другие чудеса.
- Понятие асимптот
Одним из важных этапов построения графиков функций является поиск асимптот. С асимптотами мы встречались неоднократно: при построении графиков функций , y=tgx , y=сtgx . Мы определяли их как линии, к которым «стремится» график функции, но никогда их не пересечет. Пришло время дать точное определение асимптот.
Асимптоты бывают трех видов: вертикальная, горизонтальная и наклонная. На чертеже асимптоты принято обозначать пунктирными линиями.
Рассмотрим следующий искусственно составленный график функции (рис. 16.1), на примере которого хорошо видны все виды асимптот:
Дадим определение каждому виду асимптот:
1. Прямая х=а называется вертикальной асимптотой функции , если .
2. Прямая у=с называется горизонтальной асимптотой функции , если .
3. Прямая у=kx+b называется наклонной асимптотой функции , если .
Геометрически определение наклонной асимптоты означает, что при →∞ график функции сколь угодно близко подходит к прямой у=kx+b , т.е. они практически совпадают. Разность практически одинаковых выражений стремится к нулю.
Отметим, что горизонтальные и наклонные асимптоты рассматриваются только при условии →∞. Иногда их различают на горизонтальные и наклонные асимптоты при →+∞ и →-∞.
- Алгоритм поиска асимптот
Для поиска асимптот можно использовать следующий алгоритм:
Вертикальных асимптот может быть одна, несколько или не быть совсем.
- Если с – число, то у=с – горизонтальная асимптота;
- Если с – бесконечность, то горизонтальных асимптот нет.
Если функция представляет собой отношение двух многочленов, то при наличии у функции горизонтальных асимптот наклонные асимптоты искать не будем – их нет.
Рассмотрим примеры нахождения асимптот функции:
Пример 16.1. Найдите асимптоты кривой .
Решение х -1≠0; х ≠1.
Проверим, является ли прямая х= 1 вертикальной асимптотой. Для этого вычислим предел функции в точке х= 1: .
х= 1 - вертикальная асимптота.
с = .
с = = . Т.к. с =2 (число), то у=2 – горизонтальная асимптота.
Так как функция представляет собой отношение многочленов, то при наличии горизонтальных асимптот утверждаем, что наклонных асимптот нет.
х= 1 и горизонтальную асимптоту у=2. Для наглядности график данной функции представлен на рис. 16.2.
Пример 16.2 . Найдите асимптоты кривой .
Решение . 1. Найдем область определения функции: х -2≠0; х ≠2.
Проверим, является ли прямая х= 2 вертикальной асимптотой. Для этого вычислим предел функции в точке х= 2: .
Получили, что , следовательно, х= 2 - вертикальная асимптота.
2. Для поиска горизонтальных асимптот находим : с = .
Поскольку в пределе фигурирует неопределенность , воспользуемся правилом Лопиталя: с = = . Т.к. с – бесконечность, то горизонтальных асимптот нет.
3. Для поиска наклонных асимптот находим :
Получили неопределенность вида , воспользуемся правилом Лопиталя: = =1.Итак, 1. Найдем b по формуле: .
b= = =
Получили, что b= 2. Тогда у=kx+b – наклонная асимптота. В нашем случае она имеет вид: у=x+2.
|
Лекция 17. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ И ПОСТРОЕНИЯ ГРАФИКА
В данной лекции мы подведем итог всему ранее изученному материалу. Конечная цель нашего долгого пути – уметь исследовать любую аналитически заданную функцию и строить ее график. Важными звеньями нашего исследования будут исследование функции на экстремумы, определение интервалов монотонности, выпуклости и вогнутости графика, поиск точек перегиба, асимптот графика функции.
С учетом всех вышеперечисленных аспектов приведем схему исследования функции и построения графика .
1. Найти область определения функции.
2. Исследовать функцию на четность-нечетность:
· если , то функция четная (график четной функции симметричен относительно оси Оу );
· если , то функция нечетная (график нечетной функции симметричен относительно начала координат);
· в противном случае функция ни четная, ни нечетная.
3. Исследовать функцию на периодичность (среди изучаемых нами функций периодическими могут быть только тригонометрические функции).
4. Найти точки пересечения графика функции с осями координат:
· Ох : у =0 (решаем уравнение лишь в том случае, если можем использовать известные нам методы);
· Оу : х =0.
5. Найти первую производную функции и критические точки первого рода.
6. Найти интервалы монотонности и экстремумы функции.
7. Найти вторую производную функции и критические точки второго рода.
8. Найти интервалы выпуклости-вогнутости графика функции и точки перегиба.
9. Найти асимптоты графика функции.
10. Построить график функции. При построении следует учесть случаи возможного расположения графика вблизи асимптот :
11. При необходимости выбрать контрольные точки для более точного построения.
Рассмотрим схему исследования функции и построения ее графика на конкретных примерах:
Пример 17.1 . Постройте график функции .
Решение . 1. Данная функция определена на всей числовой прямой за исключением х =3, т.к. в этой точке знаменатель обращается в ноль.
2. Для определения четности и нечетности функции найдем :
Видим, что и , следовательно, функция ни четная, ни нечетная.
3. Функция непериодическая.
4. Найдем точки пересечения с осями координат. Для нахождения точки пересечения с осью Ох примем у =0. Получим уравнение: . Итак, точка (0; 0) – точка пересечения с осями координат.
5. Найдем производную функции по правилу дифференцирования дроби: = = = = .
Для нахождения критических точек найдем точки, в которых производная функции равна 0 или не существует.
Если =0, следовательно, . Произведение тогда равно 0, когда хотя бы один из множителей равен 0: или .
х -3) 2 равен 0, т.е. не существует при х =3.
Итак, функция имеет три критические точки первого рода: ; ; .
6. На числовой оси отметим критические точки первого рода, причем точку отмечаем выколотой точкой, т.к. в ней функция не определена.
Расставляем знаки производной = на каждом промежутке:
|
|
На промежутках, где , исходная функция возрастает (при (-∞;0] ), где - убывает (при ).
Точка х =0 является точкой максимума функции. Для нахождения максимума функции найдем значение функции в точке 0: .
Точка х =6 является точкой минимума функции. Для нахождения минимума функции найдем значение функции в точке 6: .
Результаты исследований можно занести в таблицу. Число строк в таблице фиксировано и равно четырем, а число столбцов зависит от исследуемой функции. В ячейки первой строки последовательно заносят интервалы, на которые критические точки разбивают область определения функции, включая сами критические точки. Во избежание ошибок при построении точки, не принадлежащие области определения, можно в таблицу не включать.
Во второй строке таблицы расставляются знаки производной на каждом из рассматриваемых промежутков и значение производной в критических точках. В соответствии со знаками производной функции в третьей строке отмечаются промежутки возрастания, убывания, экстремумы функции.
Последняя строка служит для обозначения максимума и минимума функции.
| х | (-∞;0) | (0;3) | (3;6) | (6;+ ∞) | |||
| + | - | - | + | ||||
| f(x) | |||||||
| Выводы | max | min |
7. Найдем вторую производную функции как производную от первой производной: = =
Вынесем в числителе х -3 за скобки и выполним сокращение:
Приведем в числителе подобные слагаемые: .
Найдем критические точки второго рода: точки, в которых вторая производная функции равна нулю или не существует.
0, если =0. Данная дробь не может равняться нулю, следовательно, точек, в которых вторая производная функции равна нулю, нет.
Не существует, если знаменатель (х -3) 3 равен 0, т.е. не существует при х =3. :Ох , Оу , начало отсчета, единицы измерения по каждой оси.
Прежде чем строить график функции, нужно:
· провести асимптоты пунктирными линиями;
· отметить точки пересечения с осями координат;
|
· пользуясь полученными данными о промежутках возрастания, убывания, выпуклости и вогнутости, построить график функции. Ветви графика должны «стремиться» к асимптотам, но их не пересекать.
· проверить, соответствует ли график функции проведенному исследованию: если функция четная или нечетная, то соблюдена ли симметрия; соответствуют ли теоретически найденным промежутки возрастания и убывания, выпуклости и вогнутости, точки перегиба.
11. Для более точного построения можно выбрать несколько контрольных точек. Например, найдем значения функции в точках -2 и 7:
Корректируем график с учетом контрольных точек.
Контрольные вопросы:
- Каков алгоритм построения графика функции?
- Может ли функция иметь экстремум в точках, не принадлежащих области определении?
ГЛАВА 3. 3. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ
Сколько асимптот может быть у графика функции?
Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции. Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса - бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.
Что значит найти асимптоты графика функции?
Это значит выяснить их уравнения, ну и начертить прямые линии, если того требует условие задачи. Процесс предполагает нахождение пределов функции.
Вертикальные асимптоты графика функции
Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке функция терпит бесконечный разрыв, то прямая, заданная уравнением является вертикальной асимптотой графика.
Примечание: обратите внимание, что запись используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой - зависит от контекста.
Таким образом, чтобы установить наличие вертикальной асимптоты в точке достаточно показать, что хотя бы один из односторонних пределов бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова - любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: и ось ординат.
Из вышесказанного также следует очевидный факт: если функция непрерывна на, то вертикальные асимптоты отсутствуют. На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)
Обратное утверждение в общем случае неверно: так, функция не определена на всей числовой прямой, однако совершенно обделена асимптотами.
Наклонные асимптоты графика функции
Наклонные (как частный случай - горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше 2-х наклонных асимптот. Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при, а график арктангенса при - двумя такими асимптотами, причём различными.
Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью. Например, …правильно догадались: .
Именно так формулируется типовое задание, и оно предполагает нахождение ВСЕХ асимптот графика (вертикальных, наклонных/горизонтальных). Хотя, если быть более точным в постановке вопроса - речь идёт об исследовании на наличие асимптот (ведь таковых может и вовсе не оказаться).
Начнём с чего-нибудь простого:
Пример 1
Решение удобно разбить на два пункта:
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при , и сразу понятно, что в данной точке функция терпит бесконечный разрыв
, а прямая, заданная уравнением , является вертикальной асимптотой графика функции . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Напоминаю технику вычислений, на которой я подобно останавливался в статье непрерывность функции. Точки разрыва
. В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
.
А вот в знаменателе получается бесконечно малое отрицательное число
:
, оно и определяет судьбу предела.
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого - они ПОМОГАЮТ ПОНЯТЬ, КАК
расположен график функции и построить его КОРРЕКТНО
. Поэтому обязательно вычислим и правосторонний предел:
Вывод : односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при .
Первый предел конечен
, значит, необходимо «продолжить разговор» и найти второй предел:
Второй предел тоже конечен
.
Таким образом, наша асимптота:
Вывод : прямая, заданная уравнением является горизонтальной асимптотой графика функции при .
Для нахождения горизонтальной асимптоты можно пользоваться упрощенной формулой :
Если существует конечный предел , то прямая является горизонтальной асимптотой графика функции при .
Нетрудно заметить, что числитель и знаменатель функции одного порядка роста
, а значит, искомый предел будет конечным:
Ответ :
По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции
, то на черновике сразу же делаем набросок:
Исходя из трёх найденных пределов , попытайтесь самостоятельно прикинуть, как может располагаться график функции . Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции
, и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
Пример 2
Найти асимптоты графика функции
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта - вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдёна по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Пример 3
Найти асимптоты графика функции
Решение : Раз, два и готово:
1) Вертикальные асимптоты находятся в точках бесконечного разрыва
, поэтому нужно проверить, обращается ли знаменатель в ноль. Решим квадратное уравнение
:
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется =)
В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители
:
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
Перепишем функцию в виде 
Найдём односторонние пределы в точке :
И в точке :
Таким образом, прямые являются вертикальными асимптотами графика рассматриваемой функции.
2) Если посмотреть на функцию 
, то совершенно очевидно, что предел будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
Таким образом, прямая (ось абсцисс) является горизонтальной асимптотой графика данной функции.
Ответ :
Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:
Схематично изобразите вашу версию графика на черновике.
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции . Правильная картинка - в конце урока.
Пример 4
Найти асимптоты графика функции
Пример 5
Найти асимптоты графика функции
Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4 порядок роста знаменателя больше , чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста . В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая - через предел .
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Пример 6
Найти асимптоты графика функции
Решение : классика жанра:
1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово - отлично! Пункт №1 закрыт.
2) Проверим наличие наклонных асимптот:
Первый предел конечен
, поэтому едем дальше. В ходе вычисления второго предела для устранения неопределённости «бесконечность минус бесконечность»
приводим выражение к общему знаменателю:
Второй предел тоже конечен , следовательно, у графика рассматриваемой функции существует наклонная асимптота:
Вывод :
Таким образом, при график функции бесконечно близко
приближается к прямой :
Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы - важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
Пример 7
Найти асимптоты графика функции
Решение : комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные асимптоты. Исследуем точку .
Прямая является вертикальной асимптотой для графика при .
2) Наклонные асимптоты:
Прямая является наклонной асимптотой для графика при .
Ответ
: 
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции. Корректный чертёж в конце урока.
Пример 8
Найти асимптоты графика функции
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше - наклонной асимптоты уже не будет (например, ).
Но в жизни происходят и другие чудеса:
Пример 9
Решение
: функция непрерывна
на всей числовой прямой, значит, вертикальные асимптоты отсутствует. Но вот наклонные вполне могут быть. Проверяем:
Вспоминаю, как ещё в ВУЗе столкнулся с похожей функцией и просто не мог поверить, что у неё есть наклонная асимптота. До тех пор, пока не вычислил второй предел:
Строго говоря, здесь две неопределённости: и , но так или иначе, нужно использовать метод решения, который разобран в Примерах 5-6 статьи о пределах повышенной сложности . Умножаем и делим на сопряженное выражение, чтобы воспользоваться формулой :
Ответ :
Пожалуй, самая популярная наклонная асимптота.
До сих пор бесконечности удавалось «стричь под одну гребёнку», но бывает, что у графика функции две разные наклонные асимптоты при и при :
Пример 10
Исследовать график функции на наличие асимптот
Решение : подкоренное выражение положительно, значит, область определения - любое действительно число, и вертикальных палок быть не может.
Проверим, существуют ли наклонные асимптоты.
Если «икс» стремится к «минус бесконечности», то:
(при внесении «икса» под квадратный корень необходимо добавить знак «минус», чтобы не потерять отрицательность знаменателя)
Выглядит необычно, но здесь неопределённость «бесконечность минус бесконечность». Умножаем числитель и знаменатель на сопряженное выражение:
Таким образом, прямая является наклонной асимптотой графика при .
С «плюс бесконечностью» всё тривиальнее:
А прямая - при .
Ответ :
Если ;
, если .
Не удержусь от графического изображения:
Это одна из ветвей гиперболы
.
Не редкость, когда потенциальное наличие асимптот изначально ограничено областью определения функции :
Пример 11
Исследовать график функции на наличие асимптот
Решение
: очевидно, что 
, поэтому рассматриваем только правую полуплоскость, где есть график функции.
1) Функция непрерывна
на интервале , а значит, если вертикальная асимптота и существует, то это может быть только ось ординат. Исследуем поведение функции вблизи точки справа
:
Обратите внимание, здесь НЕТ неопределённости (на таких случаях акцентировалось внимание в начале статьи Методы решения пределов) .
Таким образом, прямая (ось ординат) является вертикальной асимптотой для графика функции при .
2) Исследование на наклонную асимптоту можно провести по полной схеме, но в статье Правила Лопитал
мы выяснили, что линейная функция более высокого порядка роста, чем логарифмическая, следовательно: 
(см. Пример 1 того же урока).
Вывод: ось абсцисс является горизонтальной асимптотой графика функции при .
Ответ :
Если ;
, если .
Чертёж для наглядности:
Интересно, что у вроде бы похожей функции асимптот нет вообще (желающие могут это проверить).
Два заключительных примера для самостоятельного изучения:
Пример 12
Исследовать график функции на наличие асимптот
Для проверки на вертикальные асимптоты сначала нужно найти область определения функции , а затем вычислить пару односторонних пределов в «подозрительных» точках. Наклонные асимптоты тоже не исключены, поскольку функция определена на «плюс» и «минус» бесконечности.
Пример 13
Исследовать график функции на наличие асимптот
А здесь могут быть только наклонные асимптоты, причём направления , следует рассмотреть отдельно.
Надеюсь, вы отыскали нужную асимптоту =)
Желаю успехов!
Решения и ответы:
Пример 2:
Решение
:
. Найдём односторонние пределы:
Прямая
является вертикальной асимптотой графика функции при
.
2) Наклонные асимптоты.
Прямая
.
Ответ
:
Чертёж
к Примеру 3:
Пример 4:
Решение
:
1) Вертикальные асимптоты. Функция терпит бесконечный разрыв в точке
. Вычислим односторонние пределы:
Примечание
: бесконечно малое отрицательное число в чётной степени равно бесконечно малому положительному числу:
.
Прямая
является вертикальной асимптотой графика функции.
2) Наклонные асимптоты.
Прямая
(ось абсцисс) является горизонтальной асимптотой графика функции при
.
Ответ
:
Асимптоты графика функции
Призрак асимптоты давно бродил по сайту чтобы, наконец, материализоваться в отдельно взятой статье и привести в особый восторг читателей, озадаченных полным исследованием функции . Нахождение асимптот графика – одна из немногих частей указанного задания, которая освещается в школьном курсе лишь в обзорном порядке, поскольку события вращаются вокруг вычисления пределов функций , а они относятся всё-таки к высшей математике. Посетители, слабо разбирающиеся в математическом анализе, намёк, думаю, понятен;-) …стоп-стоп, вы куда? Пределы – это легко!
Примеры асимптот встретились сразу же на первом уроке о графиках элементарных функций , и сейчас тема получает детальное рассмотрение.
Итак, что такое асимптота?
Представьте переменную точку , которая «ездит» по графику функции. Асимптота – это прямая , к которой неограниченно близко приближается график функции при удалении его переменной точки в бесконечность.
Примечание : определение содержательно, если вам необходима формулировка в обозначениях математического анализа, пожалуйста, обратитесь к учебнику.
На плоскости асимптоты классифицируют по их естественному расположению:
1) Вертикальные асимптоты
, которые задаются уравнением вида , где «альфа» – действительное число. Популярная представительница определяет саму ось ординат,
с приступом лёгкой тошноты вспоминаем гиперболу .
2) Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом . Иногда отдельной группой выделяют частный случай – горизонтальные асимптоты . Например, та же гипербола с асимптотой .
Резво пошло-поехало, ударим по теме короткой автоматной очередью:
Сколько асимптот может быть у графика функции?
Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции . Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса – бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.
Что значит ?
Вертикальные асимптоты графика функции
Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке функция терпит бесконечный разрыв, то прямая, заданная уравнением является вертикальной асимптотой графика.
Примечание : обратите внимание, что запись используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой – зависит от контекста.
Таким образом, чтобы установить наличие вертикальной асимптоты в точке достаточно показать, что хотя бы один
из односторонних пределов 
бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции
. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова – любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: и ось ординат (см. Графики и свойства элементарных функций
).
Из вышесказанного также следует очевидный факт: если функция непрерывна на , то вертикальные асимптоты отсутствуют . На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)
Обратное утверждение в общем случае неверно: так, функция не определена на всей числовой прямой, однако совершенно обделена асимптотами.
Наклонные асимптоты графика функции
Наклонные (как частный случай – горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше двух наклонных асимптот . Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при , а график арктангенса при – двумя такими асимптотами, причём различными.
Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью . Например, …правильно догадались: .
Общее практическое правило :
Если существуют два конечных
предела 
, то прямая является наклонной асимптотой графика функции при . Если хотя бы один
из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.
Примечание : формулы остаются справедливыми, если «икс» стремится только к «плюс бесконечности» или только к «минус бесконечности».
Покажем, что у параболы нет наклонных асимптот:
Предел бесконечен, значит, наклонная асимптота отсутствует. Заметьте, что в нахождении предела 
необходимость отпала, поскольку ответ уже получен.
Примечание
: если у вас возникли (или возникнут) трудности с пониманием знаков «плюс-минус», «минус-плюс», пожалуйста, посмотрите справку в начале урока
о бесконечно малых функциях
, где я рассказал, как правильно интерпретировать данные знаки.
Очевидно, что у любой квадратичной, кубической функции, многочлена 4-й и высших степеней также нет наклонных асимптот.
А теперь убедимся, что при у графика тоже нет наклонной асимптоты. Для раскрытия неопределённости используем правило Лопиталя
:
, что и требовалось проверить.
При функция неограниченно растёт, однако не существует такой прямой, к которой бы её график приближался бесконечно близко .
Переходим к практической части урока:
Как найти асимптоты графика функции?
Именно так формулируется типовое задание, и оно предполагает нахождение ВСЕХ асимптот графика (вертикальных, наклонных/горизонтальных). Хотя, если быть более точным в постановке вопроса – речь идёт об исследовании на наличие асимптот (ведь таковых может и вовсе не оказаться). Начнём с чего-нибудь простого:
Пример 1
Найти асимптоты графика функции
Решение удобно разбить на два пункта:
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при , и сразу понятно, что в данной точке функция терпит бесконечный разрыв
, а прямая, заданная уравнением , является вертикальной асимптотой графика функции . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Напоминаю технику вычислений, на которой я подобно останавливался в статье Непрерывность функции. Точки разрыва
. В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
.
А вот в знаменателе получается бесконечно малое отрицательное число
:
, оно и определяет судьбу предела.
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого – они ПОМОГАЮТ ПОНЯТЬ, КАК
расположен график функции и построить его КОРРЕКТНО
. Поэтому обязательно вычислим и правосторонний предел:
Вывод : односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при .
Первый предел конечен
, значит, необходимо «продолжить разговор» и найти второй предел:
Второй предел тоже конечен
.
Таким образом, наша асимптота:
Вывод : прямая, заданная уравнением является горизонтальной асимптотой графика функции при .
Для нахождения горизонтальной асимптоты
можно пользоваться упрощенной формулой
:
Если существует конечный предел , то прямая является горизонтальной асимптотой графика функции при .
Нетрудно заметить, что числитель и знаменатель функции одного порядка роста
, а значит, искомый предел будет конечным: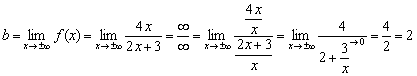
Ответ :
По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции
, то на черновике сразу же делаем набросок:
Исходя из трёх найденных пределов , попытайтесь самостоятельно прикинуть, как может располагаться график функции . Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции
, и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
Пример 2
Найти асимптоты графика функции
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта – вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдена по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Пример 3
Найти асимптоты графика функции
Решение : Раз, два и готово:
1) Вертикальные асимптоты находятся в точках бесконечного разрыва
, поэтому нужно проверить, обращается ли знаменатель в ноль. Решим квадратное уравнение
:
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется =)
В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители
:
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
Перепишем функцию в виде 
Найдём односторонние пределы в точке :
И в точке :
Таким образом, прямые являются вертикальными асимптотами графика рассматриваемой функции.
2) Если посмотреть на функцию 
, то совершенно очевидно, что предел будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
Таким образом, прямая (ось абсцисс) является горизонтальной асимптотой графика данной функции.
Ответ :
Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:
Схематично изобразите вашу версию графика на черновике.
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции . Правильная картинка – в конце урока.
Пример 4
Найти асимптоты графика функции
Пример 5
Найти асимптоты графика функции
Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4 порядок роста знаменателя больше , чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста . В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая – через предел .
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Пример 6
Найти асимптоты графика функции
Решение : классика жанра:
1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово – отлично! Пункт №1 закрыт.
2) Проверим наличие наклонных асимптот:
Первый предел конечен
, поэтому едем дальше. В ходе вычисления второго предела для устранения неопределённости «бесконечность минус бесконечность»
приводим выражение к общему знаменателю:
Второй предел тоже конечен
, следовательно, у графика рассматриваемой функции существует наклонная асимптота:
Вывод :
Таким образом, при график функции 
бесконечно близко
приближается к прямой :
Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы – важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
Пример 7
Найти асимптоты графика функции
Решение : комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные асимптоты. Исследуем точку .
Прямая является вертикальной асимптотой для графика при .
2) Наклонные асимптоты:
Прямая является наклонной асимптотой для графика при .
Ответ
: 
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции. Корректный чертёж в конце урока.
Пример 8
Найти асимптоты графика функции
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше – наклонной асимптоты уже не будет (например, ).
Но в жизни происходят и другие чудеса:
Пример 9
Пример 11
Исследовать график функции на наличие асимптот
Решение
: очевидно, что 
, поэтому рассматриваем только правую полуплоскость, где есть график функции.
Таким образом, прямая (ось ординат) является вертикальной асимптотой для графика функции при .
2) Исследование на наклонную асимптоту можно провести по полной схеме, но в статье Правила Лопиталя
мы выяснили, что линейная функция более высокого порядка роста, чем логарифмическая, следовательно: 
(см. Пример 1 того же урока).
Вывод: ось абсцисс является горизонтальной асимптотой графика функции при .
Ответ
:
, если ;
, если .
Чертёж для наглядности:
Интересно, что у вроде бы похожей функции асимптот нет вообще (желающие могут это проверить).
Два заключительных примера для самостоятельного изучения:
Пример 12
Исследовать график функции на наличие асимптот