Графический метод. Координатная плоскость (x;a). Уравнения плоскости: общее, через три точки, нормальное Y x в пространстве

Рассмотрим прямоугольную систему координат Oxyz в пространстве.

Уравнением поверхности называется такое уравнение F(x,y,z)=0, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на поверхности.

Например, сфера – это геометрическое место точек, равноудаленных от некоторой точки, называемой центром сферы. Так все точки, удовлетворяющие уравнению
лежат на сфере с центром в точке О(0.0.0) и радиусомR (Рис.1).

Координаты любой точки, не лежащей на данной сфере, не удовлетворяют этому уравнению.

Линию в пространстве можно рассматривать как линию пересечения двух поверхностей. Так на рисунке 1 пересечением сферы с плоскостью Oxy является окружность с центром в точке О и радиусом R.

Простейшей поверхностью является плоскость , простейшей линией в пространстве является прямая .

2. Плоскость в пространстве.

2.1. Уравнение плоскости по точке и нормальному вектору.

В системе координат Oxyz рассмотрим плоскость (Рис.2). Ее положение определяется заданием вектораперпендикулярного этой плоскости, и фиксированной точки
лежащей в этой плоскости. Вектор
перпендикулярный плоскости
называетсянормальным вектором (вектором-нормалью). Рассмотрим произвольную точку M(x,y,z) плоскости . Вектор
лежащий в плоскости
будет перпендикулярен вектору-нормалиИспользуя условие ортогональности векторов
получим уравнение:где

Уравнение (2.2.1 )

называется уравнением плоскости по точке и нормальному вектору.

Если в уравнении (2.1.1) раскроем скобки и перегруппируем члены, то получим уравнение илиAx + By + Cz + D = 0, где

D =
.

2.2. Общее уравнение плоскости.

Уравнение Ax + By + Cz +D = 0 (2.2.1 )

называется общим уравнением плоскости, где
- нормальный вектор.

Рассмотрим частные случаи этого уравнения.

1).D = 0. Уравнение имеет вид: Ax + By + Cz = 0. Такая плоскость проходит через начало координат. Ее нормальный вектор

2). С = 0:Ax + By + D = 0
плоскость параллельна оси oz (Рис.3).

3). B = 0: Ax + Cz + D = 0
плоскость параллельна оси oy (Рис.4).

4). A = 0: By + Cz + D = 0

плоскость параллельна оси ox (Рис.5).

5). C = D = 0: Ax + By = 0
плоскость проходит через ось oz (Рис.6).

6).B = D = 0: Ax + Cz = 0
плоскость проходит через ось oy (Рис.7).

7). A = D = 0: By + Cz = 0
плоскость проходит через ось ox (Рис.8).

8).A = B = 0: Cz + D = 0

||oz
плоскость параллельна плоскостиOxy (Рис.9).

9). B = C = 0: Ax + D = 0

||ox
плоскость

параллельна плоскостиOyz (Рис.10).

10).A = C = 0: By + D = 0

||oy
плоскость параллельна плоскостиOxz (Рис.11).

Пример 1. Составить уравнение плоскости, проходящей через точку
перпендикулярно вектору
Найти точки пересечения этой плоскости с осями координат.

Решение. По формуле (2.1.1) имеем

2x – y + 3z + 3 = 0.

Для того, чтобы найти пересечение этой плоскости с осью ox, подставим в полученное уравнение y = 0, z = 0. Имеем 2x + 3 = 0; x = – 1,5.

Точка пересечения искомой плоскости с осью ox имеет координаты:

Найдем пересечение плоскости с осью oy. Для этого возьмем x = 0; z = 0. Имеем

– y + 3 = 0 y = 3. Итак,

Для нахождения точки пересечения с осью oz возьмем x = 0; y = 0
3z + 3 = 0
z = – 1. Итак,

Ответ: 2x – y + 3z + 3 = 0,
,
,
.

Пример 2. Исследовать плоскости, заданные уравнениями:

a). 3x – y + 2z = 0

б). 2x + z – 1 = 0

в). – y + 5 = 0

Решение. а). Данная плоскость проходит через начало координат (D = 0) и имеет нормальный вектор

б). В уравнении
коэффициентB = 0. Следовательно,
Плоскость параллельна осиoy.

в). В уравнении – y + 5 = 0 коэффициенты A = 0, C = 0. Значит

Плоскость параллельна плоскости oxz.

г). Уравнение x = 0 задает плоскость oyz, так как при B = 0, C = 0 плоскость параллельна плоскости oyz, а из условия D = 0 следует, что плоскость проходит через начало координат.

Пример 3. Составить уравнение плоскости, проходящей через точку A(2,3,1) и перпендикулярной вектору
гдеB(1,0, –1), C(–2,2,0).

Решение. Найдем вектор

Вектор
является нормальным вектором искомой плоскости, проходящей через точкуA(2,3,1). По формуле (2.1.1) имеем:

– 3x + 2y + z + 6 – 6 – 1 = 0
– 3x + 2y + z – 1 = 0 3x – 2y – z + 1 = 0.

Ответ: 3x – 2y – z + 1 = 0.

2.3. Уравнение плоскости, проходящей через три точки.

Три точки, не лежащие на одной прямой, определяют единственную плоскость (см. рис. 12). Пусть точки не лежат на одной прямой. Чтобы составить уравнение плоскости, нужно знать одну точку плоскости и нормальный вектор. Точки, лежащие на плоскости, известны:
Можно взять любую. Для нахождения нормального вектора воспользуемся определением векторного произведения векторов. Пусть
Тогдаследовательно,
Зная координаты точки
и нормального векторанайдем уравнение плоскости, применяя формулу (2.1.1).

Другим способом уравнение плоскости, проходящей через три заданные точки, можно получить, используя условие компланарности трех векторов. Действительно, векторы
где M(x,y,z) – произвольная точка искомой плоскости, компланарны (см. рис.13). Следовательно, их смешанное произведение равно 0:

Применив формулу смешанного произведения в координатной форме, получим:

(2.3.1)

Пример 1. Составить уравнение плоскости, проходящей через точки

Решение. По формуле (2.3.1) имеем

Раскрыв определитель, получим:

Полученная плоскость параллельна оси oy. Ее нормальный вектор

Ответ : x + z – 4 = 0.

2.4. Угол между двумя прямыми.

Две плоскости, пересекаясь, образуют четыре двугранных угла, равных попарно (см. рис. 14). Один из двугранных углов равен углу между нормальными векторами этих плоскостей.

Пусть даны плоскости:

Их нормальные векторы имеют координаты:

Из векторной алгебры известно, что
или

(2.4.1)

Пример: Найти угол между плоскостями:

Решение: Найдем координаты нормальных векторов: По формуле (2.4.1) имеем:

Один из двугранных углов, полученных при пересечении данных плоскостей, равен
Можно найти и второй угол:

Ответ :

2.5. Условие параллельности двух плоскостей.

Пусть даны две плоскости:

и

Если эти плоскости параллельны, то их нормальные векторы

коллинеарны (см. рис.15).

Если векторы коллинеарны, то их соответствующие координаты пропорциональны:

(2.5.1 )

Верно и обратное утверждение: если нормальные векторы плоскостей коллинеарны, то плоскости параллельны.

Пример 1. Какие из указанных плоскостей параллельны:

Решение: а). Выпишем координаты нормальных векторов.

Проверим их коллинеарность:

Отсюда следует, что

б). Выпишем координаты

Проверим коллинеарность:

Векторы
не коллинеарны, плоскости
не параллельны.

Пример 2. Составить уравнение плоскости, проходящей через точку

M(2, 3, –2) параллельно плоскости

Решение: Искомая плоскость параллельна данной плоскости. Поэтому нормальный вектор плоскости можно взять за нормальный вектор искомой плоскости.
Применяя уравнение (2.1.1), получим:

Ответ:
.

Пример 3. Определить при каких a и b плоскости параллельны:

Решение: Выпишем координаты нормальных векторов:

Так как плоскости параллельны, то векторы
коллинеарны.По условию (2.5.1)
Отсюда b = – 2 ; a = 3.

Ответ: a = 3; b = –2.

2.6. Условие перпендикулярности двух плоскостей.

Если плоскости
перпендикулярны, то их нормальные векторы
тоже перпендикулярны (см. рис.16).. Отсюда следует, что их скалярное произведение равно нулю, т.е.
или в координатах:

Это условие перпендикулярности двух плоскостей. Обратное утверждение также верно, то есть, если выполняется условие (2.6.1), то векторы
следовательно,

Пример 1. Какие из указанных плоскостей перпендикулярны:

Решение: а). Запишем координаты нормальных векторов:

Проверим их ортогональность:

Отсюда следует, что

б). Запишем координаты нормальных векторов:

то есть плоскости
неперпендикулярны.

Пример 2. При каком значении m плоскости перпендикулярны

Решение: Запишем координаты нормальных векторов:

Найдем их скалярное произведение:

Так как плоскости перпендикулярны, то
Следовательно, 4 – 2m = 0;

Ответ: m = 2.

2.7. Расстояние от точки до плоскости.

Пусть дана точка
и плоскость

Расстояние от точки (см. рис.17) находим по формуле:

(2.7.1 )

Пример: Найти расстояние от точки M(3, 9, 1) до плоскости

Решение: Применяем формулу (2.7.1), где A = 1, B = – 2, C = 2, D = –3,

Ответ:

ЛЕКЦИЯ 6-7. Элементы аналитической геометрии.

Поверхности и их уравнения.

Пример 1.

Сфера .

Пример 2.

F(x,y,z)=0 (*),

Это - уравнение поверхности

Примеры :

x 2 + y 2 – z 2 = 0 (конус)

Плоскость.

Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору.

Рассмотрим плоскость в пространстве. Пусть М 0 (x 0 , y 0 , z 0) – данная точка плоскости Р, а - вектор, перпендикулярный плоскости (нормальный вектор плоскости).

(1) – векторное уравнение плоскости.

В координатной форме:

A(x - x 0) + B(y - y 0) + C(z - z 0) = 0 (2)

Получили уравнение плоскости, проходящей через заданную точку .

Общее уравнение плоскости.

Раскроем скобки в (2): Ax + By + Cz + (-Ax 0 – By 0 – Cz 0) = 0 или

Ax + By + Cz + D = 0 (3)

Полученное уравнение плоскости линейно , т.е. уравнение 1 степени относительно координат x, y, z. Поэтому плоскость – поверхность первого порядка .

Утверждение : Всякое уравнение, линейное относительно x, y, z задает плоскость.

Любая плоскость м.б. задана уравнением (3), которое называется общим уравнением плоскости.

Частные случаи общего уравнения.

а) D=0: Ax + By + Cz = 0. Т.к. координаты точки О(0, 0, 0) удовлетворяют этому уравнению, то заданная им плоскость проходит через начало координат.

б) С=0: Ax + By + D = 0. В этом случае нормальный вектор плоскости , поэтому плоскость, заданная уравнением параллельна оси OZ.

в) С=D=0: Ax + By = 0. Плоскость параллельна оси OZ (т.к. С=0) и проходит через начало координат (т.к. D=0). Значит, она проходит через ось OZ.

г) В=С=0: Ax + D = 0 или . Вектор , т.е. и . Следовательно, плоскость параллельна осям OY и OZ, т.е. параллельна плоскости YOZ и проходит через точку .

Самостоятельно рассмотреть случаи: B=0, B=D=0, A=0, A=D=0, A=C=0, A=B=0/

Уравнение плоскости, проходящей через три заданные точки.

Т.к. все четыре точки принадлежат плоскости, то данные векторы компланарны, т.е. их смешанное произведение равно нулю:

Получили уравнение плоскости, проходящей через три точки в векторной форме.

В координатной форме:

(7)

Если раскрыть определитель, то получим уравнение плоскости в виде:

Ax + By + Cz + D = 0.

Пример . Написать уравнение плоскости, проходящей через точки М 1 (1,-1,0);

М 2 (-2,3,1) и М 3 (0,0,1).

, (x - 1)·3 - (y + 1)(-2) + z·1 = 0;

3x + 2y + z – 1 = 0.

Уравнение плоскости в отрезках

Пусть дано общее уравнение плоскости Ax + By + Cz + D = 0 и D ≠ 0, т.е. плоскость не проходит через начало координат. Разделим обе части на –D: и обозначим: ; ; . Тогда

получили уравнение плоскости в отрезках .

где a, b, c – величины отрезков, отсекаемых плоскостью на осях координат.

Пример 1. Написать уравнение плоскости, проходящей через точки А(3, 0, 0);

B(0, 2, 0) и С(0, 0, -3).

a=3; b=2; c=-3 , или 2x + 3y - 2z – 6 = 0.

Пример 2. Найти величины отрезков, которые отсекает плоскость

4x – y – 3z – 12 = 0 на осях координат.

4x – y – 3z = 12 a=3, b=-12, c=-4.

Нормальное уравнение плоскости.

Пусть дана некоторая плоскость Q. Из начала координат проведем перпендикуляр ОР к плоскости. Пусть заданы |ОР|=р и вектор : . Возьмем текущую точку M(x, y, z) плоскости и вычислим скалярное произведение векторов и : .

Если спроектировать точку М на направление , то попадем в точку Р. Т.о., получим уравнение

(9).

Задание линии в пространстве.

Линию L в пространстве можно задать как пересечение двух поверхностей. Пусть точка M(x, y, z), лежащая на линии L, принадлежит как поверхности Р1, так и поверхности Р2. Тогда координаты этой точки должны удовлетворять уравнениям обеих поверхностей. Поэтому под уравнением линии L в пространстве понимают совокупность двух уравнений, каждое из которых является уравнением соответствующей поверхности:

Линии L принадлежат те и только те точки, координаты которых удовлетворяют обоим уравнениям в (*). Позже мы рассмотрим и другие способы задания линий в пространстве.

Пучок плоскостей.

Пучок плоскостей – множество всех плоскостей, проходящих через заданную прямую – ось пучка.

Чтобы задать пучок плоскостей, достаточно задать его ось. Пусть уравнение этой прямой задано в общем виде:

.

Составить уравнение пучка – значит составить уравнение, из которого можно получить при дополнительном условии уравнение любой плоскости пучка, кроме, б.м. одной. Умножим II уравнение на л и сложим с I уравнением:

A 1 x + B 1 y + C 1 z + D 1 + л(A 2 x + B 2 y + C 2 z + D 2) = 0 (1) или

(A 1 + лA 2)x + (B 1 + лB 2)y + (C 1 + лC 2)z + (D 1 + лD 2) = 0 (2).

л – параметр – число, которое может принимать действительные значения. При любом выбранном значении л уравнения (1) и (2) линейные, т.е. это – уравнения некоторой плоскости.

1. Покажем , что эта плоскость проходит через ось пучка L. Возьмем произвольную точку M 0 (x 0 , y 0 , z 0) L. Следовательно, М 0 Р 1 и М 0 Р 2 . Значит:

Следовательно, плоскость, описываемая уравнением (1) или (2) принадлежит пучку.

2. Можно доказать и обратное : всякая плоскость, проходящая через прямую L, описывается уравнением (1) при соответствующем выборе параметра л.

Пример 1 . Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + y + 5z – 1 = 0 и 2x + 3y – z + 2 = 0 и через точку М(3, 2, 1).

Записываем уравнение пучка: x + y + 5z – 1 + л(2x + 3y – z + 2) = 0. Для нахождения л учтем, что М Р:

Всякую поверхность в пространстве можно рассматривать как геометрическое место точек, обладающим некоторым свойством, общим для всех точек.

Пример 1.

Сфера – множество точек, равноудаленных от данной точки С (центра). С(x 0 ,y 0 ,z 0). По определению |СМ|=R или или . Данное уравнение выполняется для всех точек сферы и только для них. Если x 0 =0, y 0 =0, z 0 =0, то .

Аналогичным образом можно составить уравнение любой поверхности, если выбрана система координат.

Пример 2. x=0 – уравнение плоскости YOZ.

Выразив геометрическое определение поверхности через координаты ее текущей точки и собрав все слагаемые в одной части, получим равенство вида

F(x,y,z)=0 (*),

Это - уравнение поверхности , если координаты всех точек поверхности удовлетворяют данному равенству, а координаты точек, не лежащих на поверхности, не удовлетворяют.

Т.о., каждой поверхности в выбранной системе координат соответствует свое уравнение. Однако, не каждому уравнению вида (*) соответствует поверхность в смысле определения.

Примеры :

2x – y + z – 3 = 0 (плоскость)

x 2 + y 2 – z 2 = 0 (конус)

x 2 + y 2 +3 = 0 – координаты ни одной точки не удовлетворяют.

x 2 + y 2 + z 2 =0 – единственная точка (0,0,0).

x 2 = 3y 2 = 0 – прямая (ось OZ).

Все уравнения плоскости, которые разобраны в следующих пунктах могут быть получены из общего уравнения плоскости, а также приведены к общему уравнению плоскости. Таким образом, когда говорят об уравнении плоскости, то имеют в виду общее уравнение плоскости, если не оговорено иное.

Уравнение плоскости в отрезках.

Уравнение плоскости вида , где a , b и c – отличные от нуля действительные числа, называется уравнением плоскости в отрезках .

Такое название не случайно. Абсолютные величины чисел a , b и c равны длинам отрезков, которые отсекает плоскость на координатных осях Ox , Oy и Oz соответственно, считая от начала координат. Знак чисел a , b и c показывает, в каком направлении (положительном или отрицательном) следует откладывать отрезки на координатных осях.

Для примера построим в прямоугольной системе координат Oxyz плоскость, определенную уравнением плоскости в отрезках . Для этого отмечаем точку, удаленную на 5 единиц от начала координат в отрицательном направлении оси абсцисс, на 4 единицы в отрицательном направлении оси ординат и на 4 единицы в положительном направлении оси аппликат. Осталось соединить эти точки прямыми линиями. Плоскость полученного треугольника и есть плоскость, соответствующая уравнению плоскости в отрезках вида .

Для получения более полной информации обращайтесь к статье уравнение плоскости в отрезках , там показано приведение уравнения плоскости в отрезках к общему уравнению плоскости, там же Вы также найдете подробные решения характерных примеров и задач.

Нормальное уравнение плоскости.

Общее уравнение плоскости вида называют нормальным уравнением плоскости , если равна единице, то есть, , и .

Часто можно видеть, что нормальное уравнение плоскости записывают в виде . Здесь - направляющие косинусы нормального вектора данной плоскости единичной длины, то есть , а p – неотрицательное число, равное расстоянию от начала координат до плоскости.

Нормальное уравнение плоскости в прямоугольной системе координат Oxyz определяет плоскость, которая удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости . Если p=0 , то плоскость проходит через начало координат.

Приведем пример нормального уравнения плоскости.

Пусть плоскость задана в прямоугольной системе координат Oxyz общим уравнение плоскости вида . Это общее уравнение плоскости является нормальным уравнением плоскости. Действительно, и нормальный вектор этой плоскости имеет длину равную единице, так как .

Уравнение плоскости в нормальном виде позволяет находить расстояние от точки до плоскости .

Рекомендуем более детально разобраться с данным видом уравнения плоскости, посмотреть подробные решения характерных примеров и задач, а также научиться приводить общее уравнение плоскости к нормальному виду. Это Вы можете сделать, обратившись к статье .

Список литературы.

• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
• Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
• Ильин В.А., Позняк Э.Г. Аналитическая геометрия.

Чтобы получить общее уравнение плоскости, разберём плоскость, проходящую через заданную точку.

Пусть в пространстве есть три уже известные нам оси координат - Ox , Oy и Oz . Подержим лист бумаги так, чтобы он оставался плоским. Плоскостью будет сам лист и его продолжение во всех направлениях.

Пусть P произвольная плоскость в пространстве. Всякий перпендикулярный ей вектор называется вектором нормали к этой плоскости. Естественно, речь идёт о ненулевом векторе.

Если известна какая-нибудь точка плоскости P и какой-нибудь вектор нормали к ней, то этими двумя условиями плоскость в пространстве вполне определена (через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору). Общее уравнение плоскости будет иметь вид:

Итак, условия, которыми задаётся уравнение плоскости, есть. Чтобы получить само уравнение плоскости , имеющее приведённый выше вид, возьмём на плоскости P произвольную точку M с переменными координатами x , y , z . Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис. 1). Для этого, согласно условию перпендикулярности векторов, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, то есть

Вектор задан по условию. Координаты вектора найдём по формуле :

.

Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:

Так как точка M(x; y; z) выбрана на плоскости произвольно, то последнему уравнению удовлетворяют координаты любой точки, лежащей на плоскости P . Для точки N , не лежащей на заданной плоскости, , т.е. равенство (1) нарушается.

Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .

Решение. Используем формулу (1), еще раз посмотрим на неё:

В этой формуле числа A , B и C координаты вектора , а числа x 0 , y 0 и z 0 - координаты точки .

Вычисления очень простые: подставляем эти числа в формулу и получаем

Умножаем всё, что нужно умножить и складываем просто числа (которые без букв). Результат:

.

Требуемое уравнение плоскости в этом примере оказалось выражено общим уравнением первой степени относительно переменных координат x, y, z произвольной точки плоскости.

Итак, уравнение вида

называется общим уравнением плоскости .

Пример 2. Построить в прямоугольной декартовой системе координат плоскость, заданную уравнением .

Решение. Для построения плоскости необходимо и достаточно знать какие-либо три её точки, не лежащие на одной прямой, например, точки пересечения плоскости с осями координат.

Как найти эти точки? Чтобы найти точку пересечения с осью Oz , нужно в уравнение, данное в условии задачи, вместо икс и игрека подставить нули: x = y = 0 . Поэтому получаем z = 6 . Таким образом, заданная плоскость пересекает ось Oz в точке A (0; 0; 6) .

Точно так же находим точку пересечения плоскости с осью Oy . При x = z = 0 получаем y = −3 , то есть точку B (0; −3; 0) .

И, наконец, находим точку пересечения нашей плоскости с осью Ox . При y = z = 0 получим x = 2 , то есть точку C (2; 0; 0) . По трём полученным в нашем решении точкам A (0; 0; 6) , B (0; −3; 0) и C (2; 0; 0) строим заданную плоскость.

Рассмотрим теперь частные случаи общего уравнения плоскости . Это случаи, когда те или иные коэффициенты уравнения (2) обращаются в нуль.

1. При D = 0 уравнение определяет плоскость, проходящую через начало координат, так как координаты точки 0 (0; 0; 0) удовлетворяют этому уравнению.

2. При A = 0 уравнение определяет плоскость, параллельную оси Ox , поскольку вектор нормали этой плоскости перпендикулярен оси Ox (его проекция на ось Ox равна нулю). Аналогично, при B = 0 плоскость параллельная оси Oy , а при C = 0 плоскость параллельна оси Oz .

3. При A = D = 0 уравнение определяет плоскость, проходящую через ось Ox , поскольку она параллельна оси Ox (A = D = 0). Аналогично, плоскость проходит через ось Oy , а плоскость через ось Oz .

4. При A = B = 0 уравнение определяет плоскость, параллельную координатной плоскости xOy , поскольку она параллельна осям Ox (A = 0) и Oy (B = 0). Аналогично, плоскость параллельна плоскости yOz , а плоскость - плоскости xOz .

5. При A = B = D = 0 уравнение (или z = 0) определяет координатную плоскость xOy , так как она параллельна плоскости xOy (A = B = 0) и проходит через начало координат (D = 0). Аналогично, уравнение y = 0 в пространстве определяет координатную плоскость xOz , а уравнение x = 0 - координатную плоскость yOz .

Пример 3. Составить уравнение плоскости P , проходящей через ось Oy и точку .

Решение. Итак, плоскость проходит через ось Oy . Поэтому в её уравнении y = 0 и это уравнение имеет вид . Для определения коэффициентов A и C воспользуемся тем, что точка принадлежит плоскости P .

Поэтому среди её координат есть такие, которые можно подставить в уравнению плоскости, которое мы уже вывели (). Смотрим ещё раз на координаты точки:

M 0 (2; −4; 3) .

Среди них x = 2 , z = 3 . Подставляем их в уравнение общего вида и получаем уравнение для нашего частного случая:

2A + 3C = 0 .

Оставляем 2A в левой части уравнения, переносим 3C в правую часть и получаем

A = −1,5C .

Подставив найденное значение A в уравнение , получим

или .

Это и есть уравнение, требуемое в условии примера.

Решить задачу на уравнения плоскости самостоятельно, а затем посмотреть решение

Пример 4. Определить плоскость (или плоскости, если больше одной) относительно координатных осей или координатных плоскостей, если плоскость (плоскости) задана уравнением .

Решения типичных задач, которые бывают на контрольных работах - в пособии "Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке" .

Уравнение плоскости, проходящей через три точки

Как уже упоминалось, необходимым и достаточным условием для построения плоскости, кроме одной точки и вектора нормали, являются также три точки, не лежащие на одной прямой.

Пусть даны три различные точки , и , не лежащие на одной прямой. Так как указанные три точки не лежат на одной прямой, векторы и не коллинеарны, а поэтому любая точка плоскости лежит в одной плоскости с точками , и тогда и только тогда, когда векторы , и компланарны, т.е. тогда и только тогда, когда смешанное произведение этих векторов равно нулю.

Используя выражение смешанного произведения в координатах, получим уравнение плоскости

(3)

После раскрытия определителя это уравнение становится уравнением вида (2), т.е. общим уравнением плоскости.

Пример 5. Составить уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой:

и определить частный случай общего уравнения прямой, если такой имеет место.

Решение. По формуле (3) имеем:

Нормальное уравнение плоскости. Расстояние от точки до плоскости

Нормальным уравнением плоскости называется её уравнение, записанное в виде

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α 1 и α 2 , заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α 1 и α 2 равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

Пример. Определить угол между плоскостями x +2y -3z +4=0 и 2x +3y +z +8=0.

Условие параллельности двух плоскостей.

Две плоскости α 1 и α 2 параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора , параллельного этой прямой.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М 1 (x 1 , y 1 , z 1), лежащую на прямой параллельно вектору .

Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .

Векторы и коллинеарны, поэтому найдётся такое число t , что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М , лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что , и отсюда

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x , y и z и точка М перемещается по прямой.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

Пусть М 1 (x 1 , y 1 , z 1) – точка, лежащая на прямой l , и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t . Действительно, из параметрических уравнений получаем или .

Пример. Записать уравнение прямой в параметрическом виде.

Обозначим , отсюда x = 2 + 3t , y = –1 + 2t , z = 1 –t .

Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox . Тогда направляющий вектор прямой перпендикулярен Ox , следовательно, m =0. Следовательно, параметрические уравнения прямой примут вид

Исключая из уравнений параметр t , получим уравнения прямой в виде

Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.

Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz .

Примеры.

ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

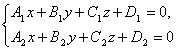
определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Примеры.

Построить прямую, заданную уравнениями

Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:

Решив эту систему, найдем точку M 1 (1;2;0).

Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz :

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на прямой и направляющий вектор прямой.

Координаты точки М 1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

.

Пример. Привести общие уравнения прямой к каноническому виду.

Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:

Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет

. Следовательно, l : .

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим